题目内容
【题目】如图所示，竖直平面内的一半径R=0．80m的光滑圆弧槽BCD，倾角为60°的斜面AB与圆弧槽BCD相切于B点，一水平面DQ与圆弧槽相接于D点．现将一质量m=0．10kg的小球从B点正上方H=1．0m高处的光滑斜面上的A点由静止释放，由B点进入圆弧轨道，从D点飞出后落在水平面上的Q点，DQ间的距离x=2．4m，球从D点飞出后的运动过程中相对于DQ水平面上升的最大高度h=0．80m，g取10m/s2，不计空气阻力．
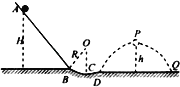
求：（1）小球经过C点时轨道对它的支持力大小FN．
（2）小球经过最高的P的速度大小vP．
（3）D点与圆心O的高度差hOD．
【答案】（1）8N（2）3．0m/s（3）0.65m
【解析】试题分析：（1）设经过C点的速度为 v1，由机械能守恒得
在C点，由牛顿第二定律有
FN﹣mg=m
代入数据解得 FN=8N
（2）设P点的速度为vP，P到Q做平抛运动，则有
竖直方向 h=
gt2
水平方向
=vPt
代入数据解得 VP=3．0m/s
（3）从A到B点的过程中，由机械能守恒得，则 mgH=
由B到D过程，由机械能守恒得：mghBD=
﹣
由D到P过程，有 mgh=﹣
代入数据解得 hBD=0．25m
由几何关系得：hOD=hOB+hBD=0．65m
练习册系列答案
相关题目
