题目内容
【题目】如图所示，滑块的质量M=2kg，开始静止在水平面上的A点，滑块与水平面间的摩擦因数为μ=0.2，与A点相距S=2.25m的B点上方有一质量m=1.2kg的小球，小球被一长为l=0.5m的轻绳挂在O点而处于静止状态．现给滑块一瞬时冲量I=10Ns，让滑块沿水平面向右运动，此后与小球发生碰撞，碰后小球恰能在竖直平面内完成完整的圆周运动（g=10m/s2）．求：
（1）滑块最终静止在距离A点多远处？
（2）因滑块与小球碰撞而损失的机械能是多少？
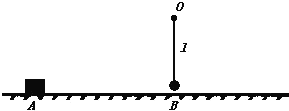
【答案】（1）2.5m；（2）0。
【解析】
（1）（2）在A点，给滑块瞬时冲量，由动量定理得：
滑块向前运动，与小球碰撞前，由动能定理得：
由动量守恒定律可得：
小球恰能完成圆周运动，到最高点，由牛顿第二定律知：
上摆过程，机械能守恒定律得：
滑块继续减速，由动能定理知：
碰撞时，由能的转化与守恒定律知：
联立以上各式解得：
=2.5m，△E=0
练习册系列答案
口算能手系列答案
相关题目
