��Ŀ����
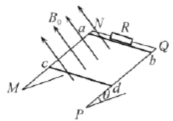
����Ŀ������ͼ��ʾ��MN��PQΪ�㹻���Ĺ⻬ƽ�е��죬���L=0.5m.����ƽ����ˮƽ���ļн�![]() = 30����NQ�AMN��NQ��������һ��
= 30����NQ�AMN��NQ��������һ��![]() �ĵ��裬��һ��ǿ�ų���ֱ�ڵ���ƽ�棬�Ÿ�Ӧǿ��Ϊ
�ĵ��裬��һ��ǿ�ų���ֱ�ڵ���ƽ�棬�Ÿ�Ӧǿ��Ϊ![]() ����һ������Ϊm=0.02kg�Ľ�����ab����NQ�����ڵ����ϣ����뵼��Ӵ����ã��������ĵ���
����һ������Ϊm=0.02kg�Ľ�����ab����NQ�����ڵ����ϣ����뵼��Ӵ����ã��������ĵ���![]() �����ಿ�ֵ��費�ƣ����ɾ�ֹ�ͷŽ��������������ص��������˶�������ʼ����NQƽ�У���������������cd��ʱ�ٶȴ�С��ʼ���ֲ��䣬cd ����NQΪ s=0.5 m��g=10m/s2��
�����ಿ�ֵ��費�ƣ����ɾ�ֹ�ͷŽ��������������ص��������˶�������ʼ����NQƽ�У���������������cd��ʱ�ٶȴ�С��ʼ���ֲ��䣬cd ����NQΪ s=0.5 m��g=10m/s2��
(1)��������ﵽ�ȶ�ʱ���ٶ��Ƕ��
(2)�������Ӿ�ֹ��ʼ���ȶ��ٶȵĹ����У�����R�ϲ����������Ƕ��٣�
(3)����������������cd����ʱ�̼���t=0,�Ӵ�ʱ�����ôŸ�Ӧǿ����С����ʹ�������в�������Ӧ��������t=1sʱ�Ÿ�Ӧǿ��ӦΪ���
���𰸡�(1)![]() (2)0.0183J(3)
(2)0.0183J(3) ![]()
��������
(1) �ڴﵽ�ȶ��ٶ�ǰ���������ļ��ٶ���С���ٶ������ﵽ�ȶ��ٶ�ʱ����
![]()
����
![]()
���ݷ����ڵ�Ÿ�Ӧ���ɣ���![]()
������ã�
![]()
(2) ����������ϵ��
![]()
����R�ϲ���������
![]()
��ã�
![]()
(3) ����·�е��ܴ�ͨ������ʱ���������в�������Ӧ��������ʱ���������ص������ȼ����˶�������ţ�ٵڶ����ɣ��У�
![]()
����λ��ʱ���ϵ��ʽ����
![]()
��tʱ�̴Ÿ�Ӧǿ��ΪB���ܴ�ͨ�����䣬�У�
![]()
��t=1sʱ���������ݽ�ã���ʱ�Ÿ�Ӧǿ�ȣ�
![]()

 �ƸԹھ��ο���ϵ�д�
�ƸԹھ��ο���ϵ�д� ������ҵ��ͬ����ϰ��ϵ�д�
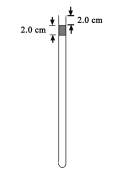
������ҵ��ͬ����ϰ��ϵ�д�����Ŀ��С��ͬѧ�������ô���ʱ�����ٶ�����ʵ��ʱ���Ӵ��µ�����ֽ����ѡ������ͼ1��ʾ��һ��ֽ������֪����ʱ��ʹ�õĵ�ԴƵ��Ϊ50Hz��ÿ�������ڼ���������ĸ���û�л������������㵽0��ľ�����ֽ������ʾ��
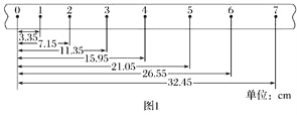

��1��Ϊ�˴ﵽʵ���Ŀ�ģ������д���ʱ����ֽ����С����ϸ�������ߡ���ѹ������Դ��Сľ�顢��ľ���⣬����Ҫ��������___
A���̶ȳ� B������̨ C��ͣ�� D����ƽ
��2��ͼ�����������ʱ����ΪT=_________s��
��3������ֽ���ṩ����Ϣ��С��ͬѧ�Ѿ�������˴���1��2��3��4��6�����������ʱС�����ٶȣ������������������¼�����5ʱС�����ٶ�v5=__________m/s���������3λ��Ч���֣�����������У�
������ | 1 | 2 | 3 | 4 | 5 | 6 |
t/s | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 |
| 0.358 | 0.400 | 0.440 | 0.485 | 0.570 |
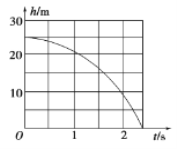
��4�����ٶ�vΪ���ᡢʱ��tΪ������ͼ2����ֽ�Ͻ���ֱ������ϵ�����ݱ��е�v��t���ݣ�������ϵ����㣬������С���˶���v��tͼ��
��________��
��5������v��tͼ���֪��С���˶��ļ��ٶȴ�СΪ_______________m/s2���������3λ��Ч���֣���