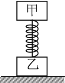题目内容
【题目】如图所示,光滑水平面上放有光滑直角斜面体,倾角θ=30°,质量M=2.5kg。平行于斜面的轻质弹簧上端固定,下端与质量m=1.5kg的铁球相连,静止时弹簧的伸长量Δl0=2cm.重力加速度g取10m/s2。现用向左的水平力F拉着斜面体向左运动,铁球与斜面体保持相对静止,当铁球对斜面体的压力为0时,求:
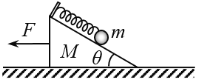
(1)水平力F的大小;
(2)弹簧的伸长量Δl.
【答案】(1)40![]() N(2)8cm
N(2)8cm
【解析】
斜面M、物体m在水平推力作用下一起加速,由牛顿第二定律可求出它们的加速度,然后结合质量可算出物体m的合力,最后利用物体的重力与合力可求出F和弹簧的弹力.
(1)当铁球与斜面体一起向左加速运动,对斜面体压力为0时,弹簧拉力为T,铁球受力如图:
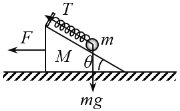
由平衡条件、牛顿第二定律得:![]()
![]()
对铁球与斜面体整体,由牛顿第二定律得:![]()
联立以上两式并代入数据得:![]()
(2)铁球静止时,弹簧拉力为T0,铁球受力如图:
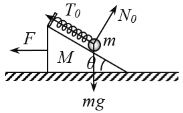
由平衡条件得: ![]()
由胡克定律得:![]()
![]()
联立以上两式并代入数据得:![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目