题目内容
2. 如图所示,质量m=1kg的小球用细线拴住,线长l=0.5m,细线所受拉力达到F=18N时就会被拉断.当小球从图地位置释放后摆到悬点的正下方时,细线恰好被拉断.若此时小球距水平地面的高度h=5m,重力加速度g=10m/s2,则小于落地处距地面上P点的距离为(P点在悬点的正下方)( )
如图所示,质量m=1kg的小球用细线拴住,线长l=0.5m,细线所受拉力达到F=18N时就会被拉断.当小球从图地位置释放后摆到悬点的正下方时,细线恰好被拉断.若此时小球距水平地面的高度h=5m,重力加速度g=10m/s2,则小于落地处距地面上P点的距离为(P点在悬点的正下方)( )| A. | 1m | B. | 2m | C. | 3m | D. | 4m |
分析 小球摆到最低点时细线恰好被拉断,细线的拉力达到F=18N,由重力和拉力的合力提供向心力求出小球摆到最低点时的速度.细线被拉断后,小球做平抛运动,由高度h求出平抛运动的时间,再求解小球落地处到地面上P点的距离.
解答 解:球摆到最低点时,有:F-mg=m$\frac{{v}^{2}}{l}$
解得小球经过最低点时的速度为:v=$\sqrt{\frac{(F-mg)l}{m}}$=$\sqrt{\frac{(18-10)×0.5}{1}}$=2m/s,
小球平抛运动的时间为:t=$\sqrt{\frac{2h}{g}}$=$\sqrt{\frac{2×5}{10}}$=1s
所以小球落地处到地面上P点的距离为:x=vt=2×1=2m.
答:小球落地处到地面上P点的距离为2m.
点评 本题是向心力知识、牛顿第二定律和平抛运动知识的综合,关键要正确分析小球摆到最低点时的受力情况,由牛顿第二定律求速度.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
15.下列关于永动机的说法中错误的是( )
| A. | 第一类永动机违反了能量守恒定律 | |
| B. | 第一类永动机违反了热力学第一定律 | |
| C. | 第二类永动机违反了能量守恒定律 | |
| D. | 第二类永动机违反了热力学第二定律 |
16.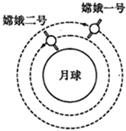 “嫦娥二号”环月飞行的高度为100km,所探测到的有关月球的数据将比环月飞行高为200km“嫦娥一号”更加详实.若两颗卫星环月的运行均可视为匀速圆周运动,运行轨道如图所示,则下列说法正确的是( )
“嫦娥二号”环月飞行的高度为100km,所探测到的有关月球的数据将比环月飞行高为200km“嫦娥一号”更加详实.若两颗卫星环月的运行均可视为匀速圆周运动,运行轨道如图所示,则下列说法正确的是( )
 “嫦娥二号”环月飞行的高度为100km,所探测到的有关月球的数据将比环月飞行高为200km“嫦娥一号”更加详实.若两颗卫星环月的运行均可视为匀速圆周运动,运行轨道如图所示,则下列说法正确的是( )
“嫦娥二号”环月飞行的高度为100km,所探测到的有关月球的数据将比环月飞行高为200km“嫦娥一号”更加详实.若两颗卫星环月的运行均可视为匀速圆周运动,运行轨道如图所示,则下列说法正确的是( )| A. | “嫦娥一号”和“嫦娥二号”绕月球匀速圆周运动的向心力由地球对它们的万有引力提供 | |
| B. | “嫦娥一号”和“嫦娥二号”的轨道平面一定过月球球心 | |
| C. | “嫦娥二号”环月运行的周期比“嫦娥一号”大 | |
| D. | “嫦娥二号”环月运行的向心加速度比“嫦娥一号”小 |
13.一物体受到5个力的作用在水平面上做匀速直线运动,若突然把其中的一个力的方向改变了30°,并且大小增大为原来的2倍,而其他力都不变,则物体可能( )
| A. | 静止 | B. | 做匀速直线运动 | ||
| C. | 做变加速曲线运动 | D. | 做匀加速直线运动 |
20. 如图所示,在气垫导轨上安装有两个光电门A、B,A、B间距离为l=30cm,为了测量滑块的加速度,在滑块上安装了一个宽度为d=1cm的遮光条,现让滑块以某一加速度通过光电门A、B,现记录了遮光条通过两光电门A、B的时间分别为0.010s、0.005s,滑块从光电门A到B的时间为0.200s,则下列说法正确的是( )
如图所示,在气垫导轨上安装有两个光电门A、B,A、B间距离为l=30cm,为了测量滑块的加速度,在滑块上安装了一个宽度为d=1cm的遮光条,现让滑块以某一加速度通过光电门A、B,现记录了遮光条通过两光电门A、B的时间分别为0.010s、0.005s,滑块从光电门A到B的时间为0.200s,则下列说法正确的是( )
 如图所示,在气垫导轨上安装有两个光电门A、B,A、B间距离为l=30cm,为了测量滑块的加速度,在滑块上安装了一个宽度为d=1cm的遮光条,现让滑块以某一加速度通过光电门A、B,现记录了遮光条通过两光电门A、B的时间分别为0.010s、0.005s,滑块从光电门A到B的时间为0.200s,则下列说法正确的是( )
如图所示,在气垫导轨上安装有两个光电门A、B,A、B间距离为l=30cm,为了测量滑块的加速度,在滑块上安装了一个宽度为d=1cm的遮光条,现让滑块以某一加速度通过光电门A、B,现记录了遮光条通过两光电门A、B的时间分别为0.010s、0.005s,滑块从光电门A到B的时间为0.200s,则下列说法正确的是( )| A. | 滑块经过A的速度为1cm/s | B. | 滑块经过B的速度为2cm/s | ||
| C. | 滑块加速度为5m/s2 | D. | 滑块A、B间的平均速度为3m/s |
11.绕地球做匀速圆周运动的卫星,离地面越近的卫星其( )
| A. | 加速度越小 | B. | 线速度越大 | C. | 角速度越小 | D. | 周期越小 |
12. 如图所示,光滑绝缘的水平面上有两个离得很近的导体环a、b.将条形磁铁沿它们的正中竖直向下移动(不到达该平面),关于a、b环的移动情况,下列说法中正确的是( )
如图所示,光滑绝缘的水平面上有两个离得很近的导体环a、b.将条形磁铁沿它们的正中竖直向下移动(不到达该平面),关于a、b环的移动情况,下列说法中正确的是( )
 如图所示,光滑绝缘的水平面上有两个离得很近的导体环a、b.将条形磁铁沿它们的正中竖直向下移动(不到达该平面),关于a、b环的移动情况,下列说法中正确的是( )
如图所示,光滑绝缘的水平面上有两个离得很近的导体环a、b.将条形磁铁沿它们的正中竖直向下移动(不到达该平面),关于a、b环的移动情况,下列说法中正确的是( )| A. | 保持静止 | B. | 相互靠近 | ||
| C. | 相互远离 | D. | 因磁体的N极在哪边未知,无法判断 |
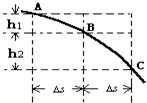 (Ⅰ)在“探究平抛运动的运动规律”的实验中,可以描绘出小球平抛运动的轨迹,实验简要步骤如下:
(Ⅰ)在“探究平抛运动的运动规律”的实验中,可以描绘出小球平抛运动的轨迹,实验简要步骤如下: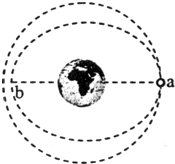 卫星携带一探测器在半径为3R(R为地球半径)的圆轨道上绕地球飞行.在a点,卫星上的辅助动力装置短暂工作,将探测器沿运动方向射出(设辅助动力装置喷出的气体质量可忽略).若探测器恰能完全脱离地球的引力,而卫星沿新的椭圆轨道运动,其近地点b距地心的距离为nR (n略小于3),求卫星与探测器的质量比.
卫星携带一探测器在半径为3R(R为地球半径)的圆轨道上绕地球飞行.在a点,卫星上的辅助动力装置短暂工作,将探测器沿运动方向射出(设辅助动力装置喷出的气体质量可忽略).若探测器恰能完全脱离地球的引力,而卫星沿新的椭圆轨道运动,其近地点b距地心的距离为nR (n略小于3),求卫星与探测器的质量比.