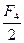题目内容
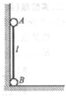
如图5-3所示,在一光滑水平面上放一个物体,人通过细绳跨过高处的定滑轮拉物体,使物体在水平面上运动,人以大小不变的速度v运动.当绳子与水平方向成θ角时,物体前进的瞬时速度是多大?

v物=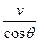
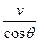
命题意图:考查分析综合及推理能力,B级要求.
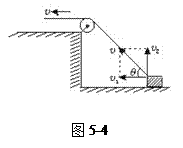

错解分析:弄不清合运动与分运动概念,将绳子收缩的速度按图5-4所示分解,从而得出错解v物=v1=vcosθ.
解题方法与技巧:解法一:应用微元法
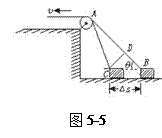
设经过时间Δt,物体前进的位移Δs1=BC,如图5-5所示.过C点作CD⊥AB,当Δt→0时,∠BAC极小,在△ACD中,可以认为AC=AD,在Δt时间内,人拉绳子的长度为Δs2=BD,即为在Δt时间内绳子收缩的长度.
由图可知:BC=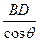 ①
①
由速度的定义:物体移动的速度为v物=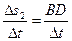 ②
②
人拉绳子的速度v=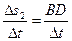 ③
③
由①②③解之:v物=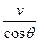
解法二:应用合运动与分运动的关系
绳子牵引物体的运动中,物体实际在水平面上运动,这个运动就是合运动,所以物体在水平面上运动的速度v物是合速度,将v物按如图5-6所示进行分解.
其中:v=v物cosθ,使绳子收缩.
v⊥=v物sinθ,使绳子绕定滑轮上的A点转动.
所以v物=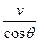
解法三:应用能量转化及守恒定律
由题意可知:人对绳子做功等于绳子对物体所做的功.
人对绳子的拉力为F,则对绳子做功的功率为P1=Fv;绳子对物体的拉力,由定滑轮的特点可知,拉力大小也为F,则绳子对物体做功的功率为P2=Fv物cosθ,因为P1=P2所以
v物=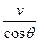



错解分析:弄不清合运动与分运动概念,将绳子收缩的速度按图5-4所示分解,从而得出错解v物=v1=vcosθ.
解题方法与技巧:解法一:应用微元法
设经过时间Δt,物体前进的位移Δs1=BC,如图5-5所示.过C点作CD⊥AB,当Δt→0时,∠BAC极小,在△ACD中,可以认为AC=AD,在Δt时间内,人拉绳子的长度为Δs2=BD,即为在Δt时间内绳子收缩的长度.
由图可知:BC=
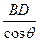 ①
①由速度的定义:物体移动的速度为v物=
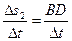 ②
②人拉绳子的速度v=
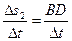 ③
③由①②③解之:v物=
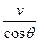
解法二:应用合运动与分运动的关系
绳子牵引物体的运动中,物体实际在水平面上运动,这个运动就是合运动,所以物体在水平面上运动的速度v物是合速度,将v物按如图5-6所示进行分解.
其中:v=v物cosθ,使绳子收缩.
v⊥=v物sinθ,使绳子绕定滑轮上的A点转动.
所以v物=
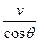
解法三:应用能量转化及守恒定律
由题意可知:人对绳子做功等于绳子对物体所做的功.
人对绳子的拉力为F,则对绳子做功的功率为P1=Fv;绳子对物体的拉力,由定滑轮的特点可知,拉力大小也为F,则绳子对物体做功的功率为P2=Fv物cosθ,因为P1=P2所以
v物=
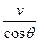

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目