题目内容
【题目】在金属板A、B间加上如图乙所示的大小不变、方向周期性变化的交变电压,其周期为T,现有电子以平行于金属板的速度v0从两板中央射入(如图甲所示).已知电子的质量为m,电荷量为e,不计电子的重力,求:
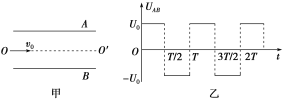
(1)若电子从t=0时刻射入,在半个周期内恰好能从A板的边缘飞出,则电子飞出时速度的大小为多少?
(2)若电子从t=0时刻射入,恰能平行于金属板飞出,则金属板至少为多长?
(3)若电子恰能从两板中央平行于板飞出,电子应从哪一时刻射入?两板间距至少为多大?
【答案】(1) ![]() (2)v0T (3)
(2)v0T (3) ![]() +k·
+k·![]() (k=0,1,2,…) T
(k=0,1,2,…) T![]()
【解析】(1)由动能定理得:e·![]() =
=![]() mv2-
mv2-![]() mv
mv
解得v=![]() .
.
(2)t=0时刻射入的电子,在垂直于极板方向上做匀加速运动,向正极板方向偏转,半个周期后电场方向反向,则继续在该方向上做匀减速运动,再经过半个周期,电场方向上的速度减到零,实际速度等于初速度v0,平行于极板,以后继续重复这样的运动.
要使电子恰能平行于金属板飞出,则在OO′方向上至少运动一个周期,故极板长至少为L=v0T.
(3)若要使电子从极板中央平行于极板飞出,则电子在电场方向上应先加速、再减速,反向加速再减速,每段时间相同,一个周期后恰好回到OO′线.可见应在t=![]() +k·
+k·![]() (k=0,1,2,…)时射入.
(k=0,1,2,…)时射入.
极板间距离要求满足在加速、减速阶段电子不打到极板上.
由牛顿第二定律有a=![]()
加速阶段运动的距离
s=![]() ·
·![]() ·
·![]() 2≤
2≤![]()
可解得d≥T![]()
故两板间距至少为T![]() .
.

练习册系列答案
相关题目