题目内容
7. 如图,在场强为E的匀强电场中,一绝缘轻质细杆L可绕点O点在竖直平面内自由转动,A端有一个带正电的小球,将细杆从水平位置自由释放,已知重力加速度
如图,在场强为E的匀强电场中,一绝缘轻质细杆L可绕点O点在竖直平面内自由转动,A端有一个带正电的小球,将细杆从水平位置自由释放,已知重力加速度为g小球的电荷量为q,质量为m.那么:
(1)小球从A到B的过程中电势能如何变化?
(2)小球在最低点时的动能Ek多大?
(3)在最低点时绝缘杆对小球的作用力FT是多少?
分析 (1)根据电场力做功判断电势能的变化.
(2)小球运动到最低点的过程中,有重力、电场力做功,根据动能定理求出小球在最低点的速率.
(3)在最低点,小球受到重力和绝缘杆的拉力,两个力的合力提供向心力,根据牛顿第二定律求出在最低点时绝缘杆对小球的作用力.
解答 解:(1)因为由A到B过程中电场力做正功,所以电势能减小.减小的电势能等于电场力做功:△EP=W=qEL,
(2)小球运动到最低点的过程中,重力和电场力做功,由动能定理得:mgL+qEL=$\frac{1}{2}m{v}^{2}-0$,
${E}_{K}=\frac{1}{2}m{v}^{2}$=mgL+qEL
(3)整理得:v=$\sqrt{\frac{2(mg+qE)L}{m}}$,即小球在最低点的速率.
在最低点由牛顿第二定律得:FT-mg=m$\frac{{v}^{2}}{L}$
将v代入公式,整理得:FT=3mg+2Eq
故最低点绝缘杆对小球的作用力大小T=3mg+2Eq.方向竖直向上.
答:(1)电势能减小,减小了qEL;
(2)小球运动到最低点的动能为mgL+qEL;
(3)在最低点时绝缘杆对小球的作用力大小为3mg+2Eq,方向竖直向上.
点评 解决本题的关键知道电场力做正功,电势能减小,电场力做负功,电势能增加.以及会用动能定理求出小球在最低点的速度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.元素X是Y的同位素,分别进行下列衰变:X$\stackrel{a}{→}$P$\stackrel{6}{→}$Q,Y$\stackrel{6}{→}$R$\stackrel{a}{→}$S,则下列说法正确的是( )
| A. | Q和S不是同位素 | B. | X和R的原子序数相同 | ||
| C. | X和R的质量数相同 | D. | R的质子数多于前述任何元素 |
2.下述说法中正确的是( )
| A. | 电场线是实际存在的,与电荷运动的轨迹是一致的 | |
| B. | 由U=Ed可知,匀强电场中的任意两点a、b间的距离越大,则两点间的电势差也一定越大 | |
| C. | 元电荷就是电子 | |
| D. | 无论正电荷还是负电荷,克服电场力做功电势能都增大 |
12. 等量异种点电荷的连线和其中垂线如图所示,现将一个带负电的检验电荷先从图中a点沿直线移到b点,再从b点沿直线移到c点.则检验电荷在此全过程中( )
等量异种点电荷的连线和其中垂线如图所示,现将一个带负电的检验电荷先从图中a点沿直线移到b点,再从b点沿直线移到c点.则检验电荷在此全过程中( )
 等量异种点电荷的连线和其中垂线如图所示,现将一个带负电的检验电荷先从图中a点沿直线移到b点,再从b点沿直线移到c点.则检验电荷在此全过程中( )
等量异种点电荷的连线和其中垂线如图所示,现将一个带负电的检验电荷先从图中a点沿直线移到b点,再从b点沿直线移到c点.则检验电荷在此全过程中( )| A. | 所受电场力的方向不变 | B. | 所受电场力逐渐增大 | ||
| C. | 电势能一直减小 | D. | 电势能先不变后减小 |
19.匀变速直线运动中,加速度a、初速度V0、末速度Vt、时间t、位移x之间关系正确的是( )
| A. | x=$\frac{1}{2}$at2 | B. | x=V0t | C. | x=v0t+$\frac{1}{2}$at2 | D. | x=(V0+Vt)$\frac{t}{2}$ |
17.在下列各组单位中,全部都是国际单位制中力学基本单位的组合是( )
| A. | N,kg,m | B. | N,kg,s | C. | kg,m,s | D. | N,m,s |
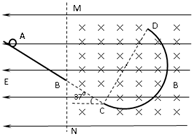 如图,与水平面成37°倾斜轨道AB,其延长线在C点与半圆轨道CD(轨道半径R=1m)相切,全部轨道为绝缘材料制成且位于竖直面内.整个空间存在水平向左的匀强电场,MN的右侧存在垂直纸面向里的匀强磁场.一个质量为0.4kg的带电小球沿斜面下滑,至B点时速度为vB=$\frac{100}{7}$m/s,接着沿直线BC(此处无轨道)运动到达C处进入半圆轨道,进入时无动能损失,且刚好到达D点.(不计空气阻力,g=10m/s2,cos37°=0.8)求:
如图,与水平面成37°倾斜轨道AB,其延长线在C点与半圆轨道CD(轨道半径R=1m)相切,全部轨道为绝缘材料制成且位于竖直面内.整个空间存在水平向左的匀强电场,MN的右侧存在垂直纸面向里的匀强磁场.一个质量为0.4kg的带电小球沿斜面下滑,至B点时速度为vB=$\frac{100}{7}$m/s,接着沿直线BC(此处无轨道)运动到达C处进入半圆轨道,进入时无动能损失,且刚好到达D点.(不计空气阻力,g=10m/s2,cos37°=0.8)求: