题目内容
17.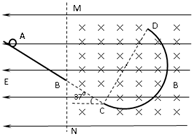 如图,与水平面成37°倾斜轨道AB,其延长线在C点与半圆轨道CD(轨道半径R=1m)相切,全部轨道为绝缘材料制成且位于竖直面内.整个空间存在水平向左的匀强电场,MN的右侧存在垂直纸面向里的匀强磁场.一个质量为0.4kg的带电小球沿斜面下滑,至B点时速度为vB=$\frac{100}{7}$m/s,接着沿直线BC(此处无轨道)运动到达C处进入半圆轨道,进入时无动能损失,且刚好到达D点.(不计空气阻力,g=10m/s2,cos37°=0.8)求:
如图,与水平面成37°倾斜轨道AB,其延长线在C点与半圆轨道CD(轨道半径R=1m)相切,全部轨道为绝缘材料制成且位于竖直面内.整个空间存在水平向左的匀强电场,MN的右侧存在垂直纸面向里的匀强磁场.一个质量为0.4kg的带电小球沿斜面下滑,至B点时速度为vB=$\frac{100}{7}$m/s,接着沿直线BC(此处无轨道)运动到达C处进入半圆轨道,进入时无动能损失,且刚好到达D点.(不计空气阻力,g=10m/s2,cos37°=0.8)求:(1)小球带何种电荷.
(2)小球在半圆轨道部分克服摩擦力所做的功.
(3)设小球从D点飞出时磁场消失,求小球离开D点后的运动轨迹与直线AC的交点到C点的距离.
分析 (1)带电粒子在只有电场的倾斜轨道上做匀加速运动后,进入电场与磁场混合的场中做匀速直线运动,重力、洛伦兹力与电场力处于平衡状态,接着沿半圆轨道运动刚好能达到D点,最后从D点做类平抛运动,此时所受到的合力正好与速度相互垂直.因此由电场力与电场强度方向可确定小球所带电性.
(2)小球在BC间做匀速直线运动.根据平衡条件和洛伦兹力公式F=qvCB求出qB.在D处,轨道对小球没有作用力,由电场力与重力的合力充当向心力,由牛顿第二定律和向心力公式列式,可求得D点的速度.小球在半圆轨道上过程,运用运动定理可得克服摩擦力做功多少.
(3)小球离开D点后作类平抛运动,由牛顿第二定律求出加速度,利用平抛运动分位移规律求解即可.
解答  解:(1)小球从B运动到C做直线运动,受力如图,电场力方向与电场强度方向相同,则小球带正电荷.
解:(1)小球从B运动到C做直线运动,受力如图,电场力方向与电场强度方向相同,则小球带正电荷.
(2)依题意可知小球在BC间做匀速直线运动.在C点的速度为:
vC=vB=$\frac{100}{7}$m/s
在BC段其受力如图所示,设重力和电场力合力为F.
F=qvCB
又:F=$\frac{mg}{cos37°}$=5N
解得:qB=$\frac{F}{{v}_{C}}$=$\frac{7}{20}$
在D处由牛顿第二定律可得:BvDq+F=m$\frac{{v}_{D}^{2}}{R}$
将qB=$\frac{7}{20}$代入上式并化简得:8${v}_{D}^{2}$-7vD-100=0
解得:vD=4m/s,vD′=-$\frac{25}{8}$m/s(舍去)
小球在CD段克服摩擦力做功Wf,由动能定理可得:
-Wf-2FR=$\frac{1}{2}m({v}_{D}^{2}-{v}_{C}^{2})$
解得:Wf=27.6J
(3)小球离开D点后作类平抛运动,其加速度为:a=$\frac{F}{m}$
由2R=$\frac{1}{2}a{t}^{2}$
得:t=$\sqrt{\frac{4mR}{F}}$=0.4$\sqrt{2}$s
交点与C点的距离:s=vDt=2.26m
答:(1)小球带正电荷.
(2)小球在半圆轨道部分克服摩擦力所做的功是27.6J.
(3)小球离开D点后的运动轨迹与直线AC的交点到C点的距离是2.26m.
点评 本题要通过分析小球的运动情况,确定其受力情况.小球从D点飞出后,正好受到重力与电场力且这两个力的合力与速度垂直,所以刚好做类平抛运动.因此可以将倾斜轨道等效看成水平面,相当于小球做平抛运动,从而可以运用平抛运动规律来处理.

| A. | 增大 | B. | 减小 | C. | 不变 | D. | 无法确定 |
 如图甲是α、β、γ三种射线穿透能力的示意图,图乙是工业上利用射线的穿透性来检查金属内部伤痕的示意图,请问图乙中的检查利用的是( )
如图甲是α、β、γ三种射线穿透能力的示意图,图乙是工业上利用射线的穿透性来检查金属内部伤痕的示意图,请问图乙中的检查利用的是( )| A. | α射线 | B. | β射线 | C. | γ射线 | D. | 三种射线都可以 |
| A. | 牛顿最早论证了重物体不会比轻物体下落得快 | |
| B. | 卡文迪许利用扭秤装置比较准确地测定了万有引力常量 | |
| C. | 牛顿根据理想斜面实验推论出,力不是维持物体速度的原因 | |
| D. | 以牛顿运动定律为基础的经典力学理论是自然界的普适规律 |
| A. | E=$\frac{F}{q}$中的场强E与电荷q无关,q 称为试探电荷 | |
| B. | E=$\frac{kq}{{r}^{2}}$中的场强E与电荷q有关,q称为场源电荷 | |
| C. | E=$\frac{F}{q}$中的F表示试探电荷受到的力 | |
| D. | E=$\frac{F}{q}$和E=$\frac{kq}{{r}^{2}}$都只对点电荷产生的电场才成立 |
| A. | 滑动摩擦力对物体一定做负功 | |
| B. | 静摩擦力对物体可能做正功 | |
| C. | 作用力的功与反作用力的功其代数和一定为零 | |
| D. | 物体速度增加时,其机械能可能减少 |
 如图所示,在倾角为θ的斜面顶端,水平抛出一小钢球,恰落到斜面底端,如果斜面长为L.(忽略空气阻力)求:
如图所示,在倾角为θ的斜面顶端,水平抛出一小钢球,恰落到斜面底端,如果斜面长为L.(忽略空气阻力)求: 质量为m的带正电小球,电荷量为q,通过一根长为L的细线系于点O上.把细线拉直,让小球从P点由静止释放,OP连线与竖直方向的夹角为α=60°.由于水平方向电场的存在,使得小球到达竖直位置A时,速度恰好等于0.求:
质量为m的带正电小球,电荷量为q,通过一根长为L的细线系于点O上.把细线拉直,让小球从P点由静止释放,OP连线与竖直方向的夹角为α=60°.由于水平方向电场的存在,使得小球到达竖直位置A时,速度恰好等于0.求: 如图,在场强为E的匀强电场中,一绝缘轻质细杆L可绕点O点在竖直平面内自由转动,A端有一个带正电的小球,将细杆从水平位置自由释放,已知重力加速度
如图,在场强为E的匀强电场中,一绝缘轻质细杆L可绕点O点在竖直平面内自由转动,A端有一个带正电的小球,将细杆从水平位置自由释放,已知重力加速度