题目内容
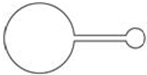
如图所示，两个半径相同的半圆形光滑轨道置于竖直平面内，左右两端点等高，分别处于沿水平方向的匀强电场和匀强磁场中．两个相同的带正电小球同时从两轨道左端最高点由静止释放．M、N为轨道的最低点，则下列说法中正确的是（ ）
A．两个小球到达轨道最低点的速度vM＜vN
B．两个小球第一次经过轨道最低点时对轨道的压力FM＞FN
C．小球第一次到达M点的时间大于小球第一次到达N点的时间
D．在磁场中小球能到达轨道的另一端最高处，在电场中小球不能到达轨道另一端最高处
【答案】分析：带电小球在磁场中运动，洛伦兹力不做功，根据动能定理求出运动到最低点的速度，从而根据牛顿第二定律求出底部对小球的支持力大小，然后进行比较．
解答：解：A、对左图，根据动能定理得，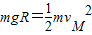
，解得
．
对右图，根据动能定理得，
，解得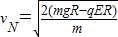
．所以vM＞vN．故A错误．
B、在最低点，对左图有：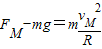
，解得FM=3mg．
对右图有：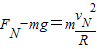
，解得FN=3mg-qE．知FM＞FN．故B正确．
C、左图在运动的过程中，只有重力做功，右图在运动的过程中，除重力做功外，还有电场力做负功，起阻碍作用，所以小球第一次到达M点的时间小于小球第一次到达N点的时间．故C错误．
D、若在磁场中小球能运动到另一端的最高处，则根据动能定理知，在电场中，电场力始终做负功，小球不能到达最高点．故D正确．
故选BD．
点评：解决本题的关键知道电场力做功和洛伦兹力做功的区别，知道洛伦兹力不做功，综合动能定理和牛顿第二定律进行求解．
解答：解：A、对左图，根据动能定理得，
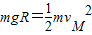，解得．对右图，根据动能定理得，
，解得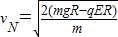．所以vM＞vN．故A错误．B、在最低点，对左图有：
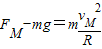，解得FM=3mg．对右图有：
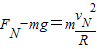，解得FN=3mg-qE．知FM＞FN．故B正确．C、左图在运动的过程中，只有重力做功，右图在运动的过程中，除重力做功外，还有电场力做负功，起阻碍作用，所以小球第一次到达M点的时间小于小球第一次到达N点的时间．故C错误．
D、若在磁场中小球能运动到另一端的最高处，则根据动能定理知，在电场中，电场力始终做负功，小球不能到达最高点．故D正确．
故选BD．
点评：解决本题的关键知道电场力做功和洛伦兹力做功的区别，知道洛伦兹力不做功，综合动能定理和牛顿第二定律进行求解．
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
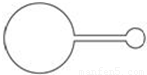
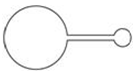
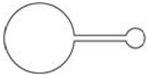如图所示，两个相连接的金属环用同样规格的导线制成，大环半径是小环半径的4倍，若穿过大环的磁场不变，穿过小环中磁感应强度随时间的变化率为k时，其路端电压为U；若穿过小环中磁场不变，而穿过大环中磁感应强度随时间的变化率为2k时，其路端电压为（ ）
、库仑力
分别为（ ）
A．
B．
D．
