题目内容
19.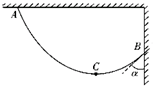 如图所示,质量为m的匀质细绳,一端系在天花板上的A点,另一端系在竖直墙壁上的B点,平衡后最低点为C点.现测得AC段绳长是BC段绳长的n倍,且绳子B端的切线与墙壁的夹角为α.则绳子在C处弹力大小为$\frac{mgtanα}{n+1}$,在A处的弹力大小为$\frac{mg}{n+1}$$\sqrt{{n}^{2}+ta{n}^{2}α}$.(重力加速度为g)
如图所示,质量为m的匀质细绳,一端系在天花板上的A点,另一端系在竖直墙壁上的B点,平衡后最低点为C点.现测得AC段绳长是BC段绳长的n倍,且绳子B端的切线与墙壁的夹角为α.则绳子在C处弹力大小为$\frac{mgtanα}{n+1}$,在A处的弹力大小为$\frac{mg}{n+1}$$\sqrt{{n}^{2}+ta{n}^{2}α}$.(重力加速度为g)
分析 先对CB段受力分析,受重力、墙壁的拉力、AC绳子对其向左的拉力,根据平衡条件求解出绳子在C处弹力大小;
再对AC绳子受力分析,受重力、BC绳子对其向右的拉力,墙壁的拉力,根据平衡条件列式求解绳子在A处弹力大小.
解答 解:对CB段受力分析,受重力、墙壁的拉力、AC绳子对其向左的拉力,如图所示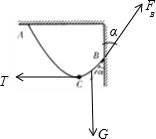
根据平衡条件,有:
FBcosα=$\frac{1}{n+1}$mg
FBsinα=T
联立解得:绳子在C处弹力大小 T=$\frac{mgtanα}{n+1}$;
再对AC绳子受力分析,受重力、BC绳子对其向右的拉力,墙壁的拉力,如图所示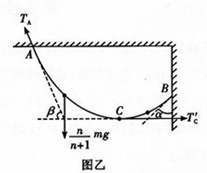
根据平衡条件,有:TAsinβ=$\frac{n}{n+1}$mg
TAcosβ=T′C
T=T′C
解得:绳子在A处的弹力大小 TA=$\frac{mg}{n+1}$$\sqrt{{n}^{2}+ta{n}^{2}α}$
故答案为:$\frac{mgtanα}{n+1}$;$\frac{mg}{n+1}$$\sqrt{{n}^{2}+ta{n}^{2}α}$.
点评 本题考查共点力的平衡条件以及隔离法的应用,解答的关键是能够灵活地选择研究对象,然后运用平衡条件列式求解.

练习册系列答案
相关题目
9.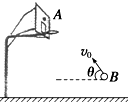 篮球运动是青年男同学最喜爱的体育运动之一,篮球投出后在空中 画出一条美丽的曲线,进入篮筐.将一篮球从地面上方B点以速度v0斜向上抛出,刚好垂直击中篮板上A点,如果有人拦截,在较远处投篮.则关于篮球的运动正确的说法是( )
篮球运动是青年男同学最喜爱的体育运动之一,篮球投出后在空中 画出一条美丽的曲线,进入篮筐.将一篮球从地面上方B点以速度v0斜向上抛出,刚好垂直击中篮板上A点,如果有人拦截,在较远处投篮.则关于篮球的运动正确的说法是( )
 篮球运动是青年男同学最喜爱的体育运动之一,篮球投出后在空中 画出一条美丽的曲线,进入篮筐.将一篮球从地面上方B点以速度v0斜向上抛出,刚好垂直击中篮板上A点,如果有人拦截,在较远处投篮.则关于篮球的运动正确的说法是( )
篮球运动是青年男同学最喜爱的体育运动之一,篮球投出后在空中 画出一条美丽的曲线,进入篮筐.将一篮球从地面上方B点以速度v0斜向上抛出,刚好垂直击中篮板上A点,如果有人拦截,在较远处投篮.则关于篮球的运动正确的说法是( )| A. | 增大抛射速度v0,同时减小抛射角θ | B. | 减小抛射速度v0,同时减小抛射角θ | ||
| C. | 增大抛射角θ,同时减小抛出速度v0 | D. | 增大抛射角θ,同时增大抛出速度v0 |
10.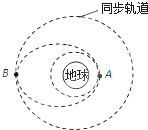 发射地球同步卫星时,先将卫星发射至距地面高度为h1的近地轨道上,在卫星经过A点时点火,实施变轨,进入远地点为B的椭圆轨道上,最后在B点再次点火,将卫星送入同步轨道,如图所示.已知同步卫星的运动周期为T,地球的半径为R,地球表面重力加速度为g,则( )
发射地球同步卫星时,先将卫星发射至距地面高度为h1的近地轨道上,在卫星经过A点时点火,实施变轨,进入远地点为B的椭圆轨道上,最后在B点再次点火,将卫星送入同步轨道,如图所示.已知同步卫星的运动周期为T,地球的半径为R,地球表面重力加速度为g,则( )
 发射地球同步卫星时,先将卫星发射至距地面高度为h1的近地轨道上,在卫星经过A点时点火,实施变轨,进入远地点为B的椭圆轨道上,最后在B点再次点火,将卫星送入同步轨道,如图所示.已知同步卫星的运动周期为T,地球的半径为R,地球表面重力加速度为g,则( )
发射地球同步卫星时,先将卫星发射至距地面高度为h1的近地轨道上,在卫星经过A点时点火,实施变轨,进入远地点为B的椭圆轨道上,最后在B点再次点火,将卫星送入同步轨道,如图所示.已知同步卫星的运动周期为T,地球的半径为R,地球表面重力加速度为g,则( )| A. | 卫星在近地圆轨道的周期最大 | |
| B. | 卫星在椭圆轨道上由A到B的过程速率逐渐减小 | |
| C. | 卫星在近地点A的加速度为$\frac{g{R}^{2}}{(R+{h}_{1})^{2}}$ | |
| D. | 远地点B距地表距离为($\frac{g{R}^{2}{T}^{2}}{4{π}^{2}}$)${\;}^{\frac{1}{3}}$ |
14.欧姆在探索通过导体的电流、电压、电阻的关系时因无电源和电流表,他利用金属在冷水和热水中产生电动势代替电源,用小磁针的偏转检测电流.具体做法是:在地磁场作用下处于水平静止的小磁针上方,平行于小磁针水平放置一直导线,当该导线中通有电流时,小磁针会发生偏转;当通过该导线电流为I时,小磁针偏转了30°;当他发现小磁针偏转了45°,则通过该直导线的电流为(直导线在某点产生的磁感应强度与通过直导线的电流成正比)( )
| A. | I | B. | 2I | C. | $\sqrt{3}$I | D. | 无法确定 |
4.已知月球半径为R,飞船在距月球表面高度为R的圆轨道上飞行,周期为T,万有引力常量为G,下列说法正确的是( )
| A. | 月球表面重力加速度为g=$\frac{32{π}^{2}R}{{T}^{2}}$ | |
| B. | 月球第一宇宙速度为$\frac{4πR}{T}$ | |
| C. | 月球密度为$\frac{3π}{G{T}^{2}}$ | |
| D. | 月球质量为$\frac{24π}{G{T}^{2}}$ |
11. 有一遥控电动玩具汽车,已知车内电动马达驱动后轮转动,现玩具汽车的后轮、前轮分别放在平板小车甲、乙上,如图所示,按动摇控器上的“前进”、“后退”键,汽车就能前进或后退,地面与甲、乙车之间的摩擦力不计,以下叙述正确的是( )
有一遥控电动玩具汽车,已知车内电动马达驱动后轮转动,现玩具汽车的后轮、前轮分别放在平板小车甲、乙上,如图所示,按动摇控器上的“前进”、“后退”键,汽车就能前进或后退,地面与甲、乙车之间的摩擦力不计,以下叙述正确的是( )
 有一遥控电动玩具汽车,已知车内电动马达驱动后轮转动,现玩具汽车的后轮、前轮分别放在平板小车甲、乙上,如图所示,按动摇控器上的“前进”、“后退”键,汽车就能前进或后退,地面与甲、乙车之间的摩擦力不计,以下叙述正确的是( )
有一遥控电动玩具汽车,已知车内电动马达驱动后轮转动,现玩具汽车的后轮、前轮分别放在平板小车甲、乙上,如图所示,按动摇控器上的“前进”、“后退”键,汽车就能前进或后退,地面与甲、乙车之间的摩擦力不计,以下叙述正确的是( )| A. | 按运摇控器上的“前进”键,乙车对前轮摩擦力向右,乙车相对地面向右运动 | |
| B. | 按运遥控器上的“前进”键,甲车对后轮摩擦力向右,甲车相对地面向左运动 | |
| C. | 按运摇控器上的“后退”键,甲车对后轮摩擦力向左,甲车相对地面向右运动 | |
| D. | 挥动摇控器上的“后退”键,乙车对前轮摩擦力向左,乙车相对地面向左运动 |
8.图所示为测量直流电阻的电路,其中线圈L的自感系数很大.在测量完毕后,为了器材的安全,将电路拆解时应( )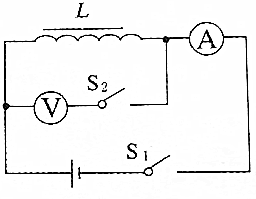

| A. | 先断开S1 | B. | 先断开S2 | C. | 先拆除电流表 | D. | 先拆除电压表 |
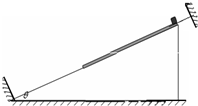 如图所示,斜面体固定在水平面上,斜面光滑,倾角为θ,斜面底端固定有与斜面垂直的挡板,木板下端离地面高H,上端放着一个细物块.木板和物块的质量均为m,相互间最大静摩擦力等于滑动摩擦力kmgsinθ(k>1),断开轻绳,木板和物块沿斜面下滑.假设木板足够长,与挡板发生碰撞时,时间极短,无动能损失,空气阻力不计.求:
如图所示,斜面体固定在水平面上,斜面光滑,倾角为θ,斜面底端固定有与斜面垂直的挡板,木板下端离地面高H,上端放着一个细物块.木板和物块的质量均为m,相互间最大静摩擦力等于滑动摩擦力kmgsinθ(k>1),断开轻绳,木板和物块沿斜面下滑.假设木板足够长,与挡板发生碰撞时,时间极短,无动能损失,空气阻力不计.求: