题目内容
10.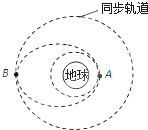 发射地球同步卫星时,先将卫星发射至距地面高度为h1的近地轨道上,在卫星经过A点时点火,实施变轨,进入远地点为B的椭圆轨道上,最后在B点再次点火,将卫星送入同步轨道,如图所示.已知同步卫星的运动周期为T,地球的半径为R,地球表面重力加速度为g,则( )
发射地球同步卫星时,先将卫星发射至距地面高度为h1的近地轨道上,在卫星经过A点时点火,实施变轨,进入远地点为B的椭圆轨道上,最后在B点再次点火,将卫星送入同步轨道,如图所示.已知同步卫星的运动周期为T,地球的半径为R,地球表面重力加速度为g,则( )| A. | 卫星在近地圆轨道的周期最大 | |
| B. | 卫星在椭圆轨道上由A到B的过程速率逐渐减小 | |
| C. | 卫星在近地点A的加速度为$\frac{g{R}^{2}}{(R+{h}_{1})^{2}}$ | |
| D. | 远地点B距地表距离为($\frac{g{R}^{2}{T}^{2}}{4{π}^{2}}$)${\;}^{\frac{1}{3}}$ |
分析 根据开普勒第三定律比较卫星的周期大小,根据万有引力做功判断卫星在椭圆轨道上运动时速率的变化.根据万有引力等于重力求出地球的质量,从而结合牛顿第二定律求出卫星在近地点A的加速度.根据万有引力提供向心力求出同步卫星的轨道半径,从而得出远地点离地表的高度.
解答 解:A、根据开普勒第三定律知,$\frac{{r}^{3}}{{T}^{2}}=k$,同步轨道的半径最大,则周期最大,故A错误.
B、卫星在椭圆轨道上由A到B的过程中,万有引力做负功,则速率逐渐减小,故B正确.
C、根据万有引力等于重力得,GM=gR2,则卫星在近地点A的加速度a=$\frac{\frac{GMm}{(R+{h}_{1})^{2}}}{m}=\frac{g{R}^{2}}{(R+{h}_{1})^{2}}$,故C正确.
D、根据$G\frac{Mm}{{r}^{2}}=mr\frac{4{π}^{2}}{{T}^{2}}$得,同步卫星的轨道半径r=$\root{3}{\frac{g{R}^{2}{T}^{2}}{4{π}^{2}}}$,则远地点B距地表距离为$\root{3}{\frac{g{R}^{2}{T}^{2}}{4{π}^{2}}}$-R,故D错误.
故选:BC.
点评 解决本题的关键掌握万有引力定律的两个重要理论:1、万有引力等于重力,2、万有引力提供向心力,并能灵活运用.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
20.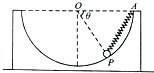 如图所示,将一劲度系数为k的轻弹簧一端固定在内壁光滑的半球形容器水平直径A处,O为球心,弹簧另一端与质量为m的小球相连,小球静止于P点.已知容器半径为R、与水平地面之间的动摩擦因数为μ,OP与水平直径的夹角为θ=60°,下列说法正确的是( )
如图所示,将一劲度系数为k的轻弹簧一端固定在内壁光滑的半球形容器水平直径A处,O为球心,弹簧另一端与质量为m的小球相连,小球静止于P点.已知容器半径为R、与水平地面之间的动摩擦因数为μ,OP与水平直径的夹角为θ=60°,下列说法正确的是( )
 如图所示,将一劲度系数为k的轻弹簧一端固定在内壁光滑的半球形容器水平直径A处,O为球心,弹簧另一端与质量为m的小球相连,小球静止于P点.已知容器半径为R、与水平地面之间的动摩擦因数为μ,OP与水平直径的夹角为θ=60°,下列说法正确的是( )
如图所示,将一劲度系数为k的轻弹簧一端固定在内壁光滑的半球形容器水平直径A处,O为球心,弹簧另一端与质量为m的小球相连,小球静止于P点.已知容器半径为R、与水平地面之间的动摩擦因数为μ,OP与水平直径的夹角为θ=60°,下列说法正确的是( )| A. | 容器与水平地面间可能有方向向左的摩擦力 | |
| B. | 容器与水平地面间一定没有摩擦力 | |
| C. | 弹簧原长为 | |
| D. | 剪断弹簧的瞬间,容器与水平地面间一定没有摩擦力 |
1.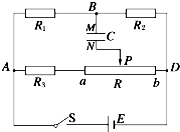 如图所示,电源内阻不计、电动势10V,R1=R2=20Ω、R3=10Ω,滑动变阻器的最大阻值R=40Ω,电容器的电容C=20μF,最初将滑动触头P置于ab中点,合上电键S,待电路稳定后,以下说法正确的是( )
如图所示,电源内阻不计、电动势10V,R1=R2=20Ω、R3=10Ω,滑动变阻器的最大阻值R=40Ω,电容器的电容C=20μF,最初将滑动触头P置于ab中点,合上电键S,待电路稳定后,以下说法正确的是( )
 如图所示,电源内阻不计、电动势10V,R1=R2=20Ω、R3=10Ω,滑动变阻器的最大阻值R=40Ω,电容器的电容C=20μF,最初将滑动触头P置于ab中点,合上电键S,待电路稳定后,以下说法正确的是( )
如图所示,电源内阻不计、电动势10V,R1=R2=20Ω、R3=10Ω,滑动变阻器的最大阻值R=40Ω,电容器的电容C=20μF,最初将滑动触头P置于ab中点,合上电键S,待电路稳定后,以下说法正确的是( )| A. | 断开S的瞬间,通过R1的电流方向左 | |
| B. | 断开S的瞬间,通过R1的电流大小为0.02 A | |
| C. | 保持S闭合,滑片P从a到b的过程中,过BM电流方向不变 | |
| D. | 保持S闭合,滑片P从a到b的过程中,过BM电流方向改变 |
5.在物理学发展过程中,观测、实验、假说和逻辑推理等方法都起到了重要作用.下列符合史实的是( )
| A. | 牛顿在前人对惯性研究基础之上,对“物体怎样才会不沿直线运动”得出这样的结论:以任何方式改变速度都需要力,进而为万有引力定律发现奠定了基础 | |
| B. | 牛顿得出了万有引力与物体质量及它们距离的关系,同时在实验室比较准确的测出了引力常量 | |
| C. | 1846年9月23日晚,德国的伽勒在勒维耶预言的位置附近发现了被后人称为“笔尖下发现的行星”--天王星 | |
| D. | 20世纪20年代,量子力学建立了,它能够很好的描述宏观物体的运动规律,并在现代科学技术中发挥了重要作用 |
15. 如图所示,两木块的质量分别为m1和m2,两轻质弹簧的劲度系数分别为k1和k2,上面木块压在上面的弹簧上(但不拴接),整个系统处于平衡状态.现缓慢向上提上面的木块,直到它刚离开上面的弹簧.在此过程中下面的木块移动的距离为( )
如图所示,两木块的质量分别为m1和m2,两轻质弹簧的劲度系数分别为k1和k2,上面木块压在上面的弹簧上(但不拴接),整个系统处于平衡状态.现缓慢向上提上面的木块,直到它刚离开上面的弹簧.在此过程中下面的木块移动的距离为( )
 如图所示,两木块的质量分别为m1和m2,两轻质弹簧的劲度系数分别为k1和k2,上面木块压在上面的弹簧上(但不拴接),整个系统处于平衡状态.现缓慢向上提上面的木块,直到它刚离开上面的弹簧.在此过程中下面的木块移动的距离为( )
如图所示,两木块的质量分别为m1和m2,两轻质弹簧的劲度系数分别为k1和k2,上面木块压在上面的弹簧上(但不拴接),整个系统处于平衡状态.现缓慢向上提上面的木块,直到它刚离开上面的弹簧.在此过程中下面的木块移动的距离为( )| A. | $\frac{{{m_1}g}}{k_1}$ | B. | $\frac{{{m_2}g}}{k_1}$ | C. | $\frac{{{m_1}g}}{k_2}$ | D. | $\frac{{{m_2}g}}{k_2}$ |
2.根据牛顿第一定律,我们可以得到如下的推论( )
| A. | 静止的物体一定不受其它外力作用 | |
| B. | 力停止作用后,物体就慢慢停下来 | |
| C. | 物体的运动状态发生了改变,必定受到外力的作用 | |
| D. | 惯性是物体保持匀速运动或静止状态的特性,质量是惯性大小的唯一量度 |
 如图所示,一个质量m=10kg的物体放在粗糙水平地面上.对物体施加一个F=50N的水平拉力,使物体由静止开始做匀加速直线运动.若物块与地面间的动摩擦因数为0.2求:
如图所示,一个质量m=10kg的物体放在粗糙水平地面上.对物体施加一个F=50N的水平拉力,使物体由静止开始做匀加速直线运动.若物块与地面间的动摩擦因数为0.2求: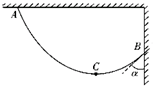 如图所示,质量为m的匀质细绳,一端系在天花板上的A点,另一端系在竖直墙壁上的B点,平衡后最低点为C点.现测得AC段绳长是BC段绳长的n倍,且绳子B端的切线与墙壁的夹角为α.则绳子在C处弹力大小为$\frac{mgtanα}{n+1}$,在A处的弹力大小为$\frac{mg}{n+1}$$\sqrt{{n}^{2}+ta{n}^{2}α}$.(重力加速度为g)
如图所示,质量为m的匀质细绳,一端系在天花板上的A点,另一端系在竖直墙壁上的B点,平衡后最低点为C点.现测得AC段绳长是BC段绳长的n倍,且绳子B端的切线与墙壁的夹角为α.则绳子在C处弹力大小为$\frac{mgtanα}{n+1}$,在A处的弹力大小为$\frac{mg}{n+1}$$\sqrt{{n}^{2}+ta{n}^{2}α}$.(重力加速度为g)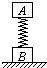 如图所示,木块A和B的质量均为m,连接在一根轻弹簧的两端,B放在水平桌面上时,弹簧处于直立位置,若压下木块A后突然放开,当A上升并达到最大速度时,B对桌面的压力为多少?B从桌面跳起时A的加速度为多少?
如图所示,木块A和B的质量均为m,连接在一根轻弹簧的两端,B放在水平桌面上时,弹簧处于直立位置,若压下木块A后突然放开,当A上升并达到最大速度时,B对桌面的压力为多少?B从桌面跳起时A的加速度为多少?