题目内容
(12分)如图所示,在平面直角坐标系xOy中,第Ⅰ象限内有平行于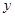 轴的匀强电场,方向沿y轴正方向;第Ⅳ象限的正三角形abc区域内有匀强磁场,方向垂直于xOy平面向里。正三角形边长为L,且
轴的匀强电场,方向沿y轴正方向;第Ⅳ象限的正三角形abc区域内有匀强磁场,方向垂直于xOy平面向里。正三角形边长为L,且 边与y轴平行。质量为m、电荷量为q的粒子,从y轴上的P(0,h)点,以大小为v0的速度沿x轴正方向射入电场,通过电场后从x轴上的a(2h,0)点进入第Ⅳ象限,又经过磁场从y轴上的某点进入第Ⅲ象限,且速度与y轴负方向成45°角,不计粒子所受的重力。试求:
边与y轴平行。质量为m、电荷量为q的粒子,从y轴上的P(0,h)点,以大小为v0的速度沿x轴正方向射入电场,通过电场后从x轴上的a(2h,0)点进入第Ⅳ象限,又经过磁场从y轴上的某点进入第Ⅲ象限,且速度与y轴负方向成45°角,不计粒子所受的重力。试求:
(1)电场强度的大小。
(2)粒子到达a点时速度的大小和方向。
(3)△abc区域内磁场的磁感应强度的最小值。
(1) (2)
(2) v0 速度方向指向第Ⅳ象限且与x轴正方向成45°角
v0 速度方向指向第Ⅳ象限且与x轴正方向成45°角
(3)
解析试题分析:(1)设电场强度为E,粒子在电场中运动的加速度为a,历时为t。由题意得:
qE =" ma" 1分
2h = v0t 1分
h =  at2 1分
at2 1分
联立以上各式,解得:
E= 1分
1分
(2)设粒子到达a点时的速度大小为v,方向与x轴正方向成θ角;沿负y方向的分速度为vy。则:
vy = at 1分
v =  1分
1分
tanθ=  1分
1分
联立以上各式,解得:
v=  v0 1分
v0 1分
θ = 45° 1分
速度方向指向第Ⅳ象限且与x轴正方向成45°角
(3)设粒子在磁场中做匀速圆周运动的半径为r。因洛伦兹力提供向心力,故由牛顿第二定律得:
qvB = m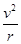 1分
1分
分析可知,当粒子从b点射出时,磁场的磁感应强度为最小值,设为Bmin,运动轨迹如图所示。
有几何关系可得:
2·rcosθ=L 1分
联立解得:Bmin=  1分
1分
考点:带电粒子在电场和磁场中的运动.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案如图甲所示是电容器充、放电电路.配合电流传感器,可以捕捉瞬间的电流变化,并通过计算机画出电流随时间变化的图象.实验中选用直流8 V电源,电容器选用电解电容器.先使单刀双掷开关S与1端相连,电源向电容器充电,这个过程可瞬间完成.然后把单刀双掷开关S掷向2端,电容器通过电阻R放电,传感器将电流传入计算机,图象上显示出放电电流随时间变化的I-t曲线,如图乙所示.以下说法正确的是( )
| A.电解电容器用氧化膜做电介质,由于氧化膜很薄,所以电容较小 |
| B.随着放电过程的进行,该电容器两极板间电压逐渐减小 |
| C.由传感器所记录的该放电电流图象可以估算出该过程中电容器的放电电荷量 |
| D.通过本实验可以估算出该电容器的电容值 |



 时刻释放该带电粒子,释放瞬间粒子加速度的大小;
时刻释放该带电粒子,释放瞬间粒子加速度的大小;


 cm,板长L=1.0cm,带电粒子质量m=2.0×10-25kg,电量q=8.0×10-18C,入射速度v =
cm,板长L=1.0cm,带电粒子质量m=2.0×10-25kg,电量q=8.0×10-18C,入射速度v = ×105m/s.若能在荧光屏上观察到亮点,试求粒子在磁场中运动的轨道半径r,并确定磁场区域的半径R应满足的条件.
×105m/s.若能在荧光屏上观察到亮点,试求粒子在磁场中运动的轨道半径r,并确定磁场区域的半径R应满足的条件. 时刻以速度v0射入电场,要使该电子能通过平行金属板,试确定U0应满足的条件.
时刻以速度v0射入电场,要使该电子能通过平行金属板,试确定U0应满足的条件.