题目内容
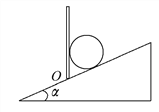
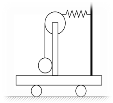
【题目】如图为某自动投放器的示意图,其下半部AB是一长为R的竖直管道,上半部BC是半径为R的四分之一圆弧光滑轨道,AB管内有一原长为R、下端固定的轻质弹簧.投放时,若将弹簧长度压缩了0.5R后锁定,在弹簧上端放置一个可视为质点且质量为m的小球,解除锁定,弹簧可将小球弹射出去.当小球到达顶端C时,对轨道壁的压力恰好为零,不计一切阻力,且锁定和解除锁定时,均不改变弹簧的弹性势能.已知重力加速度为g,求:

(1)小球到达顶端C时的速度大小v1;
(2)弹簧压缩了0.5R时的弹性势能Ep1;
(3)若将弹簧压缩了0.6R时,弹簧弹性势能为Ep2=![]() Ep1,小球落地点离OO′的水平距离s是多少?
Ep1,小球落地点离OO′的水平距离s是多少?
【答案】(1)鱼饵到达管口C时的速度大小![]() ;(2)弹簧压缩到0.5R时的弹性势能Ep=2mgR;(3)若将弹簧压缩了0.6R时,弹簧弹性势能为Ep2=
;(2)弹簧压缩到0.5R时的弹性势能Ep=2mgR;(3)若将弹簧压缩了0.6R时,弹簧弹性势能为Ep2=![]() Ep1,小球落地点离OO′的水平距离是4.2R
Ep1,小球落地点离OO′的水平距离是4.2R
【解析】
试题分析:(1)质量为m的鱼饵到达管口C时做圆周运动的向心力,完全由重力提供,
则mg=m![]() …①
…①
由①式解得:v1=![]() …②
…②
(2)从弹簧释放到最高点C的过程中,弹簧的弹性势能全部转化为鱼饵的机械能,由系统的机械能守恒定律有Ep=mg(0.5R+R)+ ![]() mv12 …③
mv12 …③
由②③式解得:Ep=2mgR…④
(3)设其到达管口C时速度大小为v2,由机械能守恒定律得:Ep2=mg(0.6R+R)+![]() mv22 …⑤
mv22 …⑤
鱼饵离开管口C后做平抛运动,设经过t时间落到水面上,离OO'的水平距离为x,由平抛运动规律有:x=v2t+R…⑥ h=2R=![]() gt2 ⑦
gt2 ⑦
由⑤⑥⑦式解得:x=4.2R

练习册系列答案
相关题目