题目内容
15. 如图所示,一个质量为0.4kg的小物块从高h=0.05m的坡面顶端由静止释放,滑到水平台上,滑行一段距离后,从边缘O点水平飞出,击中平台右下侧挡板上的P点.现以O为原点在竖直面内建立如图所示的平面直角坐标系,挡板的形状满足方程y=x2-6(单位:m),不计一切摩擦和空气阻力,g=10m/s2,则下列说法正确的是( )
如图所示,一个质量为0.4kg的小物块从高h=0.05m的坡面顶端由静止释放,滑到水平台上,滑行一段距离后,从边缘O点水平飞出,击中平台右下侧挡板上的P点.现以O为原点在竖直面内建立如图所示的平面直角坐标系,挡板的形状满足方程y=x2-6(单位:m),不计一切摩擦和空气阻力,g=10m/s2,则下列说法正确的是( )| A. | 小物块从水平台上O点飞出的速度大小为1m/s | |
| B. | 小物块从O点运动列P点的时间为2s | |
| C. | 小物块刚到P点时速度方向与水平方向夹角的正切值等于5 | |
| D. | 小物块刚到P点时速度的大小为10m/s |
分析 对小物块由动能定理可以求出物块的速度,物块做平抛运动,应用平抛运动规律可以求出P点的速度大小与方向,及时间,从而即可求解.
解答 解:A、对小物块,从释放至到达O点的过程中,由动能定理得:
mgh=$\frac{1}{2}$mv2-0,
代入数据解得:v=$\sqrt{2gh}$=$\sqrt{2×10×0.05}$=1m/s.故A正确;
B、小物块从O点水平抛出做平抛运动,
竖直方向:y=-$\frac{1}{2}$gt2,
水平方向:x=v0t,
解得:y=-5x2;
又有:y=x2-6,
联立解得:x=1m,y=-5m,
根据h=$\frac{1}{2}$gt2,解得:t=$\sqrt{\frac{2h}{g}}=\sqrt{\frac{2×5}{10}}$s=1s;故B错误;
C、那么竖直方向的速度大小vy=gt=10×1=10m/s;
设刚到P点时速度方向与水平方向夹角为θ,则有:tan=$\frac{{v}_{y}}{{v}_{0}}$=$\frac{10}{1}$=10,故C错误;
D、根据速度的合成法则,则有刚到P点时速度的大小为v=$\sqrt{{v}_{y}^{2}+{v}_{0}^{2}}$=$\sqrt{1{0}^{2}+{1}^{2}}$=$\sqrt{101}$m/s,故D错误;
故选:A.
点评 本题考查了求速度与坐标问题,分析清楚小球的运动过程、应用动能定理与平抛运动规律即可正确解题.

练习册系列答案
相关题目
6.“神舟十号”飞船与“天宫一号”目标飞行器在离地面343km的近似圆形的轨道上,成功进行了交会对接.对接轨道所处的空间存在极其稀薄的大气.下列说法正确的是( )
| A. | 在对接前,如不加干预,在运行一段时间后,“天宫一号”的动能可能会增加 | |
| B. | 在对接前,如不加干预,“天宫一号”的轨道高度将缓慢增加 | |
| C. | 在对接时,两者运行速度的大小都应大于第一宇宙速度 | |
| D. | 航天员在“天宫一号”内的“私人睡眠站”中睡觉时处于平衡状态 |
3. 如图所示,甲、乙两船的总质量(包括船、人和货物)分别为10m、12m,两船沿同一直线同一方向运动,速率分别为2v0、v0,为避免两船相撞,乙船上的人将一质量为m的货物沿水平方向抛向甲船,甲船上的人将货物接住.不计水的阻力.则抛出货物的最小速率是( )
如图所示,甲、乙两船的总质量(包括船、人和货物)分别为10m、12m,两船沿同一直线同一方向运动,速率分别为2v0、v0,为避免两船相撞,乙船上的人将一质量为m的货物沿水平方向抛向甲船,甲船上的人将货物接住.不计水的阻力.则抛出货物的最小速率是( )
 如图所示,甲、乙两船的总质量(包括船、人和货物)分别为10m、12m,两船沿同一直线同一方向运动,速率分别为2v0、v0,为避免两船相撞,乙船上的人将一质量为m的货物沿水平方向抛向甲船,甲船上的人将货物接住.不计水的阻力.则抛出货物的最小速率是( )
如图所示,甲、乙两船的总质量(包括船、人和货物)分别为10m、12m,两船沿同一直线同一方向运动,速率分别为2v0、v0,为避免两船相撞,乙船上的人将一质量为m的货物沿水平方向抛向甲船,甲船上的人将货物接住.不计水的阻力.则抛出货物的最小速率是( )| A. | v0 | B. | 2v0 | C. | 3v0 | D. | 4v0 |
10.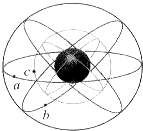 2014年11月中国的北斗系统成为第三个被联合国认可的海上卫星导航系统,其导航系统中部分卫星运动轨道如图所示.己知a、b、c为圆形轨道( )
2014年11月中国的北斗系统成为第三个被联合国认可的海上卫星导航系统,其导航系统中部分卫星运动轨道如图所示.己知a、b、c为圆形轨道( )
 2014年11月中国的北斗系统成为第三个被联合国认可的海上卫星导航系统,其导航系统中部分卫星运动轨道如图所示.己知a、b、c为圆形轨道( )
2014年11月中国的北斗系统成为第三个被联合国认可的海上卫星导航系统,其导航系统中部分卫星运动轨道如图所示.己知a、b、c为圆形轨道( )| A. | 在轨道a、b运行的两颗卫星加速度相同 | |
| B. | 在轨道a、b运行的两颗卫星受到地球的引力一样大 | |
| C. | 卫星在轨道c、a的运行周期Ta>Tc | |
| D. | 卫星在轨道c、a的运行速度va>vc |
20.一人造卫星在距离地球表面高度为h的圆形轨道上运行时的周期为T,若测得地球半径为R,则该人造卫星离开地球时的最小发射速度为( )
| A. | $\frac{2π(R+h)}{T}$$\sqrt{\frac{R}{R+H}}$ | B. | $\frac{(R+h)}{T}$$\sqrt{\frac{R+h}{R}}$ | C. | $\frac{2πT}{R+h}$$\sqrt{\frac{R+h}{R}}$ | D. | $\frac{2π(R+h)}{T}$$\sqrt{\frac{R+h}{R}}$ |
 如图所示,光滑斜面长为a,宽为b,倾角为θ.一物块沿斜面上方顶点P水平射入,而从右下方顶点Q离开斜面,求物块入射的初速度为多少?.
如图所示,光滑斜面长为a,宽为b,倾角为θ.一物块沿斜面上方顶点P水平射入,而从右下方顶点Q离开斜面,求物块入射的初速度为多少?. 如图所示,光滑水平面上有A、B、C三个物块,其质量分别为mA=2kg,mB=1kg,mC=1kg.现用一轻弹簧将A、B两物块连接,并用力缓慢压缩弹簧使A、B两物块靠近,此过程外力做功W=108J(弹簧仍处于弹性限度内),然后同时释放A、B,弹簧开始逐渐变长,当弹簧刚好恢复原长时,C恰以4m/s的速度迎面与B发生碰撞并粘连在一起.求:
如图所示,光滑水平面上有A、B、C三个物块,其质量分别为mA=2kg,mB=1kg,mC=1kg.现用一轻弹簧将A、B两物块连接,并用力缓慢压缩弹簧使A、B两物块靠近,此过程外力做功W=108J(弹簧仍处于弹性限度内),然后同时释放A、B,弹簧开始逐渐变长,当弹簧刚好恢复原长时,C恰以4m/s的速度迎面与B发生碰撞并粘连在一起.求: 如图,绝热气缸A与导热气缸B横截面积相同,均固定于地面,由刚性杆连接的绝热活塞与两气缸间均无摩擦.两气缸内都装有处于平衡状态的理想气体,开始时体积均为V0、温度均为T0,缓慢加热A中气体,停止加热达到稳定后,A中气体压强变为原来的1.2倍,设环境温度始终保持不变,求气缸A中气体的体积VA和温度TA.
如图,绝热气缸A与导热气缸B横截面积相同,均固定于地面,由刚性杆连接的绝热活塞与两气缸间均无摩擦.两气缸内都装有处于平衡状态的理想气体,开始时体积均为V0、温度均为T0,缓慢加热A中气体,停止加热达到稳定后,A中气体压强变为原来的1.2倍,设环境温度始终保持不变,求气缸A中气体的体积VA和温度TA.