题目内容
20.一人造卫星在距离地球表面高度为h的圆形轨道上运行时的周期为T,若测得地球半径为R,则该人造卫星离开地球时的最小发射速度为( )| A. | $\frac{2π(R+h)}{T}$$\sqrt{\frac{R}{R+H}}$ | B. | $\frac{(R+h)}{T}$$\sqrt{\frac{R+h}{R}}$ | C. | $\frac{2πT}{R+h}$$\sqrt{\frac{R+h}{R}}$ | D. | $\frac{2π(R+h)}{T}$$\sqrt{\frac{R+h}{R}}$ |
分析 万有引力提供向心力有G$\frac{Mm}{{R}^{2}}$=m$\frac{{v}^{2}}{R}$,地球表面的物体受到的重力等于万有引力有G$\frac{Mm}{{R}^{2}}$=mg,由以上二式可以解得飞船在轨道上发射的最小速度大小.
再利用万有引力提供向心力有G$\frac{Mm}{(R+h)^{2}}$=m($\frac{2π}{T}$)2(R+h),可以解得飞船运行的周期T与重力加速度关系,从而即可求解.
解答 解:根据万有引力提供向心力,有:G$\frac{Mm}{{R}^{2}}$=m$\frac{{v}^{2}}{R}$,所以:v=$\sqrt{\frac{GM}{R}}$
又因为地球表面的物体受到的重力等于万有引力G$\frac{Mm}{{R}^{2}}$=mg,有:GM=R2g
根据万有引力提供向心力,有:G$\frac{Mm}{(R+h)^{2}}$=m($\frac{2π}{T}$)2(R+h),
所以:v=$\frac{2π(R+h)}{T}\sqrt{\frac{R+h}{R}}$,故D正确,ABC错误;
故选:D.
点评 本题要掌握天体运动中两个重要的关系:万有引力提供向心力;星球表面的物体受到的重力等于万有引力.

练习册系列答案
相关题目
10.如图是街头变压器通过降压给用户供电的示意图.变压器的输入电压是市区电网的电压,假设负载变化时输入电压保持不变.输出电压通过输电线输送给用户,两条输电线的总电阻用R0表示,R代表各户用中电器电阻.忽略变压器上的能量损失,不计电压表、电流表的内阻对电路的影响.当用户的用电器增加时,下列说法正确的是( )


| A. | 输出功率变小 | |
| B. | 输入功率不变 | |
| C. | 电压表1读数不变,电流表1读数增大 | |
| D. | 电压表2读数增大,电流表2读数增大 |
11.下列说法中正确的是( )
| A. | 雨水没有透过布雨伞是因为液体表面存在张力 | |
| B. | 分子间的距离r增大,分子间的作用力做负功,分子势能增大 | |
| C. | 气体自发的扩散运动总是沿着分子热运动的无序性增大的方向进行 | |
| D. | 悬浮在液体中的微粒越大,在某一瞬间撞击它的液体分子数越多,布朗运动越明显 |
15. 如图所示,一个质量为0.4kg的小物块从高h=0.05m的坡面顶端由静止释放,滑到水平台上,滑行一段距离后,从边缘O点水平飞出,击中平台右下侧挡板上的P点.现以O为原点在竖直面内建立如图所示的平面直角坐标系,挡板的形状满足方程y=x2-6(单位:m),不计一切摩擦和空气阻力,g=10m/s2,则下列说法正确的是( )
如图所示,一个质量为0.4kg的小物块从高h=0.05m的坡面顶端由静止释放,滑到水平台上,滑行一段距离后,从边缘O点水平飞出,击中平台右下侧挡板上的P点.现以O为原点在竖直面内建立如图所示的平面直角坐标系,挡板的形状满足方程y=x2-6(单位:m),不计一切摩擦和空气阻力,g=10m/s2,则下列说法正确的是( )
 如图所示,一个质量为0.4kg的小物块从高h=0.05m的坡面顶端由静止释放,滑到水平台上,滑行一段距离后,从边缘O点水平飞出,击中平台右下侧挡板上的P点.现以O为原点在竖直面内建立如图所示的平面直角坐标系,挡板的形状满足方程y=x2-6(单位:m),不计一切摩擦和空气阻力,g=10m/s2,则下列说法正确的是( )
如图所示,一个质量为0.4kg的小物块从高h=0.05m的坡面顶端由静止释放,滑到水平台上,滑行一段距离后,从边缘O点水平飞出,击中平台右下侧挡板上的P点.现以O为原点在竖直面内建立如图所示的平面直角坐标系,挡板的形状满足方程y=x2-6(单位:m),不计一切摩擦和空气阻力,g=10m/s2,则下列说法正确的是( )| A. | 小物块从水平台上O点飞出的速度大小为1m/s | |
| B. | 小物块从O点运动列P点的时间为2s | |
| C. | 小物块刚到P点时速度方向与水平方向夹角的正切值等于5 | |
| D. | 小物块刚到P点时速度的大小为10m/s |
5. 两个质量均为M的星体,其连线的垂直平分线为HN,O为其连线的中点,如图所示,一个质量为m的物体从O沿OH方向运动,则它受到的万有引力大小变化情况是( )
两个质量均为M的星体,其连线的垂直平分线为HN,O为其连线的中点,如图所示,一个质量为m的物体从O沿OH方向运动,则它受到的万有引力大小变化情况是( )
 两个质量均为M的星体,其连线的垂直平分线为HN,O为其连线的中点,如图所示,一个质量为m的物体从O沿OH方向运动,则它受到的万有引力大小变化情况是( )
两个质量均为M的星体,其连线的垂直平分线为HN,O为其连线的中点,如图所示,一个质量为m的物体从O沿OH方向运动,则它受到的万有引力大小变化情况是( )| A. | 一直增大 | B. | 一直减小 | C. | 先减小,后增大 | D. | 先增大,后减小 |
12.为了测量某行星的质量和半径,宇航员记录了登陆舱在该行星表面附近做圆周运动的周期T,登陆舱在行星表面着陆后,用弹簧称称量一个质量为m的砝码读数为N.已知引力常量为G.则下列计算中错误的是( )
| A. | 该行星的质量为$\frac{{N}^{3}{T}^{4}}{16G{P}^{4}{m}^{3}}$ | B. | 该行星的半径为$\frac{4{π}^{2}N{T}^{2}}{m}$ | ||
| C. | 该行星的密度为$\frac{3π}{G{T}^{2}}$ | D. | 该行星的第一宇宙速度为$\frac{NT}{2πm}$ |
9.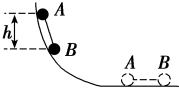 如图所示,两个质量均为m的完全相同的小球A和B用轻杆连接,由静止从曲面上释放至滑到水平面的过程中,不计一切摩擦,则杆对A球做的功为( )
如图所示,两个质量均为m的完全相同的小球A和B用轻杆连接,由静止从曲面上释放至滑到水平面的过程中,不计一切摩擦,则杆对A球做的功为( )
 如图所示,两个质量均为m的完全相同的小球A和B用轻杆连接,由静止从曲面上释放至滑到水平面的过程中,不计一切摩擦,则杆对A球做的功为( )
如图所示,两个质量均为m的完全相同的小球A和B用轻杆连接,由静止从曲面上释放至滑到水平面的过程中,不计一切摩擦,则杆对A球做的功为( )| A. | $\frac{1}{2}$mgh | B. | -$\frac{1}{2}$mgh | C. | mgh | D. | -mgh |
12.下列说法正确的是( )
| A. | 作用在物体上的滑动摩擦力只能使物体减速,不可能使物体加速 | |
| B. | 伽利略开创了实验研究和逻辑推理相结合的科学方法,并利用这种方法发现:忽略空气阻力的情况下,重物与轻物下落得同样快 | |
| C. | 速度变化越快的物体惯性越大,匀速运动或静止时没有惯性 | |
| D. | 磁感线总是从磁体的N极出发终止于磁体的S极 |