题目内容
14. 如图所示,质量m=4kg的物体(可视为质点)用细绳拴住,放在水平传送带的右端,物体和传送带之间的动摩擦因数μ=0.4,传送带的长度l=2m,当传送带以v=4m/s的速度做逆时针转动时,绳与水平方向的夹角θ=37°.已知:g=l0m/s2,sin37°=0.6,cos37°=0.8.求:
如图所示,质量m=4kg的物体(可视为质点)用细绳拴住,放在水平传送带的右端,物体和传送带之间的动摩擦因数μ=0.4,传送带的长度l=2m,当传送带以v=4m/s的速度做逆时针转动时,绳与水平方向的夹角θ=37°.已知:g=l0m/s2,sin37°=0.6,cos37°=0.8.求:(1)传送带稳定运动时绳子的拉力T;
(2)某时刻剪断绳子,求物体做匀加速直线运动的时间;
(3)如果提高传送带的运行速率,物体就能被较快地传送到左处,求物体从图示位置处传送到左端处的最短时间和传送带对应的最小运行速率.
分析 (1)物块受重力、支持力、拉力和滑动摩擦力处于平衡,根据共点力平衡,运用正交分解求出绳子拉力的大小.
(2)剪断绳子,物块先做匀加速直线运动,当速度达到传送带速度时,判定物块是否到达传送带的左端,然后结合牛顿第二定律和运动学公式求出物体运动到传送带的左端的时间.
(3)物块一直做加速运动时的时间最短,由此结合运动学的公式与牛顿第二定律即可解答.
解答 解:(1)传送带稳定运动时,物体处于平衡状态:
Tcosθ=μ(mg-Tsinθ)
解得:T=15.4N
(2)剪断绳子后,根据牛顿第二定律:μmg=ma
求得:a=4 m/s2
匀加速的时间:t1=$\frac{v}{a}$=1s
位移:s1=$\frac{1}{2}a{t^2}$=2 m 可知此时物体恰好到达传送带的左端.
(3)由(2)的解答可知,在传送带以v=4m/s的速度做逆时针转动时,物块一直做加速运动,所以到达传送带左端的时间恰好为最短的时间,传送带的速度恰好是物块以最短时间到达左端的最小速度.
答:(1)传送带稳定运动时绳子的拉力T为15.4N;
(2)某时刻剪断绳子,物体做匀加速直线运动的时间是1s;
(3)物体从图示位置处传送到左端处的最短时间就是1s,传送带对应的最小运行速率是4m/s.
点评 解决本题的关键能够根据物体的受力,判断物体的运动,理清整个过程中物块的运动状况,结合牛顿第二定律和运动学公式进行求解.

练习册系列答案
相关题目
2. 如图所示,为实线是某一点电荷所形成的一簇电场线,a、b、c 三条虚线分别为三个电荷量大小相等的带电粒子a、b、c以相同的速度从O点射入电场的运动轨迹,其中b虚线为一圆弧,ABC为三条虚线与电场线的交点,不计粒子重力,则以下说法正确的是.( )
如图所示,为实线是某一点电荷所形成的一簇电场线,a、b、c 三条虚线分别为三个电荷量大小相等的带电粒子a、b、c以相同的速度从O点射入电场的运动轨迹,其中b虚线为一圆弧,ABC为三条虚线与电场线的交点,不计粒子重力,则以下说法正确的是.( )
 如图所示,为实线是某一点电荷所形成的一簇电场线,a、b、c 三条虚线分别为三个电荷量大小相等的带电粒子a、b、c以相同的速度从O点射入电场的运动轨迹,其中b虚线为一圆弧,ABC为三条虚线与电场线的交点,不计粒子重力,则以下说法正确的是.( )
如图所示,为实线是某一点电荷所形成的一簇电场线,a、b、c 三条虚线分别为三个电荷量大小相等的带电粒子a、b、c以相同的速度从O点射入电场的运动轨迹,其中b虚线为一圆弧,ABC为三条虚线与电场线的交点,不计粒子重力,则以下说法正确的是.( )| A. | ABC三点场强大小关系是:EA<EB<EC | |
| B. | a一定带正电,b和c一定带负电 | |
| C. | a粒子的速率越来越小,b粒子的速率不变,c粒子的速率越来越大 | |
| D. | b粒子的质量大于c粒子的质量 |
4.在一个点电荷形成的电场中,关于电场强度和电势的说法中正确的是( )
| A. | 没有任何两点电场强度相同 | |
| B. | 可以找到很多电场强度相同的点 | |
| C. | 没有任何两点电势相等 | |
| D. | 零电势点没有确定,无法确定电势是否相等 |
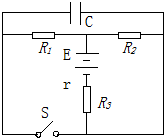 如图所示电路中,R1=3Ω,R2=6Ω,R3=1.5Ω,C=20μF,当开关S断开时,电源所释放的总功率为2W;当开关S闭合时,电源所释放的总功率为4W,求:S断开和闭合时,电容器所带的电量各是多少?
如图所示电路中,R1=3Ω,R2=6Ω,R3=1.5Ω,C=20μF,当开关S断开时,电源所释放的总功率为2W;当开关S闭合时,电源所释放的总功率为4W,求:S断开和闭合时,电容器所带的电量各是多少?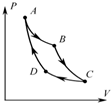 如图所示,一定质量的理想气体从状态A依次经过状态B、C和D后再回到状态A.其中,A→B和C→D为等温过程,B→C和D→A为绝热过程(气体与外界无热量交换). 这就是著名的“卡诺循环”.
如图所示,一定质量的理想气体从状态A依次经过状态B、C和D后再回到状态A.其中,A→B和C→D为等温过程,B→C和D→A为绝热过程(气体与外界无热量交换). 这就是著名的“卡诺循环”.