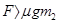题目内容
如图所示,在动摩擦因数μ=0.2的水平面上有一质量m=lkg的小球,一水平放置的轻弹簧一端与墙相连,另一端与小球相连,一不可伸长的轻质细绳一端与小球相连,另一端固定在天花板上,细绳与竖直方向成45°角,此时小球处于静止状态,且水平面对小球的弹力恰好为零。取g=10m/s2,小球所受的最大静摩擦力等于滑动摩擦力,则在烧断轻绳的瞬间,下列说法正确的是( )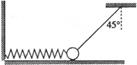
| A.小球所受合外力为零 |
| B.小球的加速度大小为10m/s2,方向向左 |
| C.小球的加速度大小为8m/s2,方向向左 |
| D.小球所受合力的方向沿左下方,与竖直方向成45°角 |
C
解析试题分析:当小球处于静止状态时,水平面对小球的弹力恰为零,所以弹簧对小球的弹力大小F=mg,绳对小球的拉力T=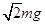 ,在烧断轻绳的瞬间,弹簧的弹力F大小不能突变,水平面对小球的支持力大小突变为N=mg,所以小球的加速度大小a=
,在烧断轻绳的瞬间,弹簧的弹力F大小不能突变,水平面对小球的支持力大小突变为N=mg,所以小球的加速度大小a=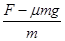 =8m/s2,方向向左,故选项C正确。
=8m/s2,方向向左,故选项C正确。
考点:本题主要考查了轻绳与轻弹簧模型的施力特征,以及牛顿第二定律的应用问题,属于中档题。

 一线名师提优试卷系列答案
一线名师提优试卷系列答案如图所示,甲、乙两车均在光滑的水平面上,质量都是 ,人的质量都是
,人的质量都是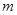 ,甲车上人用力
,甲车上人用力 推车,乙车上的人用等大的力
推车,乙车上的人用等大的力 拉绳子(绳与轮的质量和摩擦均不计);人与车始终保持相对静止.下列说法正确的是
拉绳子(绳与轮的质量和摩擦均不计);人与车始终保持相对静止.下列说法正确的是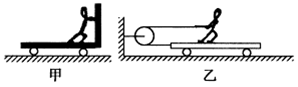
A.甲车的加速度大小为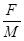 |
| B.甲车的加速度大小为0 |
C.乙车的加速度大小为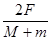 |
| D.乙车的加速度大小为0 |
如图所示,三个质量相同,形状相同的斜面,放在地面上。另有三个质量相同的小物体分别从斜面顶端沿斜面滑下。由于小物体跟斜面间的摩擦不同,第一个小物体匀加速下滑;第二个小物体匀速下滑;第三个小物体以初速v0匀减速下滑。三个斜面都不动。则下滑过程中斜面对地面的压力大小顺序是( )
| A.N1 = N2 = N3 | B.N1 < N2 < N3 | C.N1 > N2 > N3 | D.N1 < N2 = N3 |
一汽车在路面情况相同的公路上直线行驶,下面关于车速、惯性、质量和滑行路程的讨论,正确的是
| A.车速越大,它的惯性越大 |
| B.质量越大,它的惯性越大 |
| C.车速越大,刹车后滑行的路程越长 |
| D.车速越大,刹车后滑行的路程越长,所以惯性越大 |
如图所示,竖直光滑杆上套有一个小球和两根弹簧,两弹簧的一端各与小球相连,另一端分别用销钉M、N固定于杆上,小球处于静止状态,设拔去销钉M瞬间,小球加速度的大小为12 m /s2,若不拔去销钉M而拔去销钉N瞬间,小球的加速度可能是(取g="10m" /s2)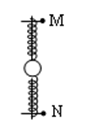
| A.22 m /s2,竖直向上 | B.22 m /s2,竖直向下 |
| C.2 m /s2,竖直向上 | D.2 m /s2,竖直向下 |
如图所示,位于光滑固定斜面上的小物块P受到一水平向右的推力F的作用。已知物块P沿斜面加速下滑。现保持F的方向不变,使其减小,则加速度( )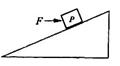
| A.一定变小 | B.一定变大 |
| C.一定不变 | D.可能变小,可能变大,也可能不变 |

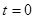 时速度为零,若用
时速度为零,若用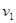 、
、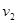 、
、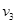 、
、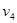 分别表示上述四种受力情况下物体在
分别表示上述四种受力情况下物体在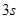 末的速率,则这四个速率中最大的是( )
末的速率,则这四个速率中最大的是( )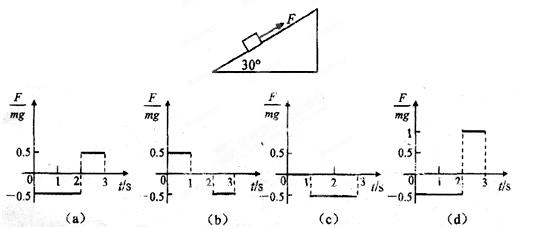

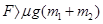 B.
B.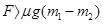
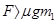 D.
D.