题目内容
3.用如图1所示的装置进行实验,可以研究物体的加速度与质量及所受合外力的关系.实验过程中,将砝码盘及其中砝码所受总重力视为研究物体(小车)昕受的合外力(拉力)的大小.
①甲同学用这套装置探究“物体质量一定时.其加速度与合外力大小的关系”.
a.他首先保证小车的质量不变.多次改变小车所受合外力(拉力)的大小.分别根据打点计时器打出的纸带计算出小车运动的加速度.并利用测量的数据画出a-F图线进行分析.
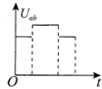
b.若发现图线在横轴上的截距OA较大(如图2甲).明显超出了偶然误差的范围,其原因是由于没有平衡摩擦力或平衡摩擦力不够
c.若发现图线不是一条直线,而向下弯曲(如图2乙),其原因是由于不满足小车的质量远小于砝码盘中及其中砝码的总质量
②乙同学用这套装置设计了研究“在合外力一定的条件下,物体的加速度与其质量间的关系”的实验方案,其主要实验步骤如下:
a.先不加挂砝码盘,在小车上加装一定质量的砝码,调整木板右端的高度,用手轻推一下小车,直到打点计时器打出一系列间隔均匀的点迹.
b.按住小车,按图2方式加挂砝码盘,打开打点计时器电源,释放小车,获得带有打上了点迹的纸带,在纸带上标出小车中砝码的质量m.
c.按住小车,仅改变小车上加装砝码的质量,更换纸带重复上述步骤a、b.
d.求出与不同m相对应的加速度a.
以小车上加装砝码的质量m为横坐标,$\frac{1}{a}$为纵坐标,在坐标纸上做出去$\frac{1}{a}$-m关系图线如图3所示.设图中直线的斜率为k,在纵轴上的截距为b,则根据牛顿第二定律可知,小车受到的拉力为$\frac{1}{k}$,小车的质量为$\frac{b}{k}$.
分析 ①甲图象表明在小车的拉力为0时,合外力大于0,说明平衡摩擦力过度.
乙图象说明在拉力大于0时,物体的加速度为0,说明绳子的拉力被摩擦力平衡了,即没有平衡摩擦力或平衡摩擦力不足
设绳子上拉力为F,对小车根据牛顿第二定律有:F=Ma,对砂桶和砂有:mg-F=ma,由此解得:F=$\frac{mg}{1+\frac{m}{M}}$,由此可知当M>>时,砂和砂桶的重力等于绳子的拉力,据此根据该实验实验误差产生的原因即可正确解答.
②根据牛顿第二定律写出$\frac{1}{a}$与小车上砝码质量m的表达式,然后结合斜率与截距概念求解即可.
解答 解:①甲图象表明在小车的拉力为0时,小车的加速度大于0,说明合外力大于0,说明平衡摩擦力过渡,即把长木板的末端抬得过高了.故A错误B正确.
乙图象说明在拉力大于0时,物体的加速度为0,说明合外力为0,即绳子的拉力被摩擦力平衡了,即没有平衡摩擦力或平衡摩擦力不足,也就是没有将长木板的末端抬高或抬高不够.
随着$\frac{1}{M}$增大,小车质量在减小,因此小车质量不再满足远大于砂和小砂桶的质量,加速度不可能一直均匀增大,加速度的增大幅度将逐渐减小,最后趋近于定值g,
②设小车的质量为m',则有F=(m+m')a,
变形得$\frac{1}{a}$=$\frac{1}{F}$m+$\frac{m′}{F}$,
所以$\frac{1}{a}$-m图象的斜率为$\frac{1}{F}$=k,
所以作用力F=$\frac{1}{k}$,
$\frac{1}{a}$-m图象的截距为$\frac{m′}{F}$=b,
所以m′=$\frac{b}{k}$.
故答案为:①没有平衡摩擦力或平衡摩擦力不够,不满足小车的质量远小于砝码盘中及其中砝码的总质量;②$\frac{1}{k}$,$\frac{b}{k}$.
点评 解决实验问题首先要掌握该实验原理,了解实验的操作步骤和数据处理以及注意事项,尤其是理解平衡摩擦力和M>>m的操作和要求的含义.
遇到涉及图象的问题时,要先根据物理规律写出关于纵轴与横轴的函数表达式,再根据斜率和截距的概念求解即可.

 利用频闪照相装置拍摄一列沿x轴向右传播的简谐横波某部分区域内的波形,如图所示,实线是在t=0时刻的波形图,虚线是在t=0.04s时刻的波形图.则x=20cm的质点第一次出现波谷的时刻是( )
利用频闪照相装置拍摄一列沿x轴向右传播的简谐横波某部分区域内的波形,如图所示,实线是在t=0时刻的波形图,虚线是在t=0.04s时刻的波形图.则x=20cm的质点第一次出现波谷的时刻是( )| A. | 0.42 s | B. | 0.38 s | C. | 0.36s | D. | 0.30 s |
 氢原子能级的示意图如图所示,以下选项描述了当氢原子跃迁时的情况,其中跃迁过程辐射出光子、且光子的波长最长的是( )
氢原子能级的示意图如图所示,以下选项描述了当氢原子跃迁时的情况,其中跃迁过程辐射出光子、且光子的波长最长的是( )| A. | 从n=3的能级向n=1的能级跃迁 | B. | 从n=4的能级向n=2的能级跃迁 | ||
| C. | 从n=1的能级向n=3的能级跃迁 | D. | 从n=2的能级向n=4的能级跃迁 |

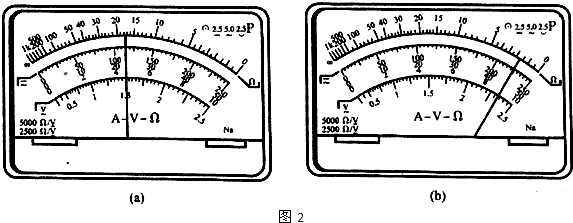
①分别用多用电表欧姆挡的“×100”、“×1k”两挡粗测水样的电阻值时,表盘上指针如图2(a)、(b)所示,则所测水样的电阻约为1750Ω.
②为更精确地测量所取水样的电阻,该小组使用实验器材:
A.电流表(量程0~l0mA,电阻RA约为10Ω)
B.电压表(量程0~15V,电阻R.约为30kΩ)
C.滑动变阻器(最大电阻10Ω,额定电流1.5A)
D.电源(12V,内阻约2Ω)
E.开关一只、导线若干
请在图3实物图中完成剩余的电路连接.
③正确连接电路后,闭合开关,测量得到如下数据:
| 组别 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| U/V | 5.1 | 5.8 | 7.0 | 8.1 | 9.0 | 10.0 | 11.0 |
| I/mA | 2.9 | 3.3 | 4.0 | 5.0 | 5.1 | 5.7 | 6.3 |
⑤在处理数据过程中,发现其中一组数据误差偏大,它是第4(用表格中“组别”的序号表示)组.
 一质量为m,所带电荷量为-q的粒子以速度v0射入两带电平行极板间,如图所示,已知两极板间的电势差为U,距离为d,不计重力,则粒子穿出电场时的速度为( )
一质量为m,所带电荷量为-q的粒子以速度v0射入两带电平行极板间,如图所示,已知两极板间的电势差为U,距离为d,不计重力,则粒子穿出电场时的速度为( )| A. | $\sqrt{\frac{2U}{d}}$ | B. | v0+$\sqrt{\frac{2qU}{m}}$ | C. | v0+$\sqrt{\frac{2qU}{d}}$ | D. | $\sqrt{\frac{m{v}_{0}^{2}+2qU}{m}}$ |
 利用如图所示装置可以做力学中的许多实验.
利用如图所示装置可以做力学中的许多实验. 为了较准确地测量某电子元件的电阻,某实验小组做如下测量:
为了较准确地测量某电子元件的电阻,某实验小组做如下测量: 有一个推矿泉水瓶的游戏节目,规则是:选手们从起点开始用力推瓶一段时间后,放手让瓶向前滑动,若瓶最后停在桌上有效区域内,视为成功;若瓶最后未停在桌上有效区域内或在滑行过程中倒下,均视为失败.其简化模型如图所示,AC是长度为L1=5m的水平桌面,选手们可将瓶子放在A点,从A点开始用一恒定不变的水平推力推瓶,BC为有效区域.已知BC长度L2=1m,瓶子质量m=0.5kg,瓶子与桌面间的动摩擦因数μ=0.4.某选手作用在瓶子上的水平推力F=20N,瓶子沿AC做直线运动,假设瓶子可视为质点,g取10m/s2,那么该选手要想游戏获得成功,试问:
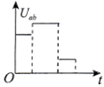
有一个推矿泉水瓶的游戏节目,规则是:选手们从起点开始用力推瓶一段时间后,放手让瓶向前滑动,若瓶最后停在桌上有效区域内,视为成功;若瓶最后未停在桌上有效区域内或在滑行过程中倒下,均视为失败.其简化模型如图所示,AC是长度为L1=5m的水平桌面,选手们可将瓶子放在A点,从A点开始用一恒定不变的水平推力推瓶,BC为有效区域.已知BC长度L2=1m,瓶子质量m=0.5kg,瓶子与桌面间的动摩擦因数μ=0.4.某选手作用在瓶子上的水平推力F=20N,瓶子沿AC做直线运动,假设瓶子可视为质点,g取10m/s2,那么该选手要想游戏获得成功,试问: 如图所示,由同种材料制成的粗细均匀的正方形金属线框,以恒定速度通过有理想边界的匀强磁场,线框的边长小于有界磁场区域的宽度.开始时线框的ab边恰与磁场的边界重合,整个运动过程中线框的运动方向始终与ab边垂直,线框平面始终与磁场方向垂直.则下图中可能定性反映出线框中a、b两点间的电势差Uab随时间变化的是( )
如图所示,由同种材料制成的粗细均匀的正方形金属线框,以恒定速度通过有理想边界的匀强磁场,线框的边长小于有界磁场区域的宽度.开始时线框的ab边恰与磁场的边界重合,整个运动过程中线框的运动方向始终与ab边垂直,线框平面始终与磁场方向垂直.则下图中可能定性反映出线框中a、b两点间的电势差Uab随时间变化的是( )