题目内容
13. 一质量为m,所带电荷量为-q的粒子以速度v0射入两带电平行极板间,如图所示,已知两极板间的电势差为U,距离为d,不计重力,则粒子穿出电场时的速度为( )
一质量为m,所带电荷量为-q的粒子以速度v0射入两带电平行极板间,如图所示,已知两极板间的电势差为U,距离为d,不计重力,则粒子穿出电场时的速度为( )| A. | $\sqrt{\frac{2U}{d}}$ | B. | v0+$\sqrt{\frac{2qU}{m}}$ | C. | v0+$\sqrt{\frac{2qU}{d}}$ | D. | $\sqrt{\frac{m{v}_{0}^{2}+2qU}{m}}$ |
分析 负电荷在电场中受力的方向与电场的方向相反,所以带电粒子在电场中做加速运动,电场力做正功,由动能定理即可求出.
解答 解:负电荷在电场中运动的过程中电场力做正功,由动能定理得:
$qU=\frac{1}{2}m{v}^{2}-\frac{1}{2}m{v}_{0}^{2}$
所以:v=$\sqrt{\frac{m{v}_{0}^{2}+2qU}{m}}$
故选:D
点评 带电粒子在电场中做加速运动的过程中,电场力做的功与路径无关,仅仅与两点之间的电势差有关.所以带电粒子在电场中的加速,常常使用动能定理来解答,而不是用牛顿运动定律来解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.如图1所示,单匝矩形线框相邻两边分别长为L和2L,从中线OO′处对折,且保持折角θ=90°不变.如图2所示,使线框在水平向右的匀强磁场中以角速度ω绕竖直方向的OO′轴匀速转动.匀强磁场的磁感应强度大小为B,线框电阻为R,从图2所示位置(线框的OO′CD部分与中性面重合)开始计时,取A→B→C→D→A为线框中感应电流的正方向,下列说法正确的是( )

| A. | 线框中感应电流i随时间t的变化关系是i=$\frac{{\sqrt{2}B{L^2}ω}}{R}$cos(ωt+$\frac{π}{4}$) | |
| B. | 线框中感应电流i随时间t的变化关系是i=$\frac{{B{L^2}ω}}{R}$•cosωt | |
| C. | 在t=0时刻,线框中的感应电流最大 | |
| D. | 从0~$\frac{π}{2ω}$时间内,感应电流方向改变1次 |
19. 质量相同的甲、乙两物体放在相同的光滑水平地面上,分别在水平力F1、F2的作用下从同一地点,沿同一方向,同时运动,其v-t图象如图所示,下列判断正确的是( )
质量相同的甲、乙两物体放在相同的光滑水平地面上,分别在水平力F1、F2的作用下从同一地点,沿同一方向,同时运动,其v-t图象如图所示,下列判断正确的是( )
 质量相同的甲、乙两物体放在相同的光滑水平地面上,分别在水平力F1、F2的作用下从同一地点,沿同一方向,同时运动,其v-t图象如图所示,下列判断正确的是( )
质量相同的甲、乙两物体放在相同的光滑水平地面上,分别在水平力F1、F2的作用下从同一地点,沿同一方向,同时运动,其v-t图象如图所示,下列判断正确的是( )| A. | 在0~2s内,F1越来越大 | |
| B. | 4s末甲、乙两物体动能相同,由此可知F1=F2 | |
| C. | 4~6s内两者逐渐靠近 | |
| D. | 0~6s内两者在前进方向上的最大距离为4m |

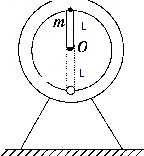 如图所示,在电机的转轴O处固定一根长为L的轻杆,在轻杆的另一端固定一质量为m的铁球.电机启动后,轻杆以角速度ω绕轴O在竖直面内匀速转动,求地面对电机的最大支持力和最小支持力的差值△F.
如图所示,在电机的转轴O处固定一根长为L的轻杆,在轻杆的另一端固定一质量为m的铁球.电机启动后,轻杆以角速度ω绕轴O在竖直面内匀速转动,求地面对电机的最大支持力和最小支持力的差值△F. 如图,质量为M=1kg的物块静止在桌面边缘,桌面离水平地面的高度为h=1.8m.一质量为m=20g的子弹以水平速度v0=20m/s射入物块,在很短的时间内以水平速度v1=10m/s穿出木块.重力加速度g取10m/s2,求:
如图,质量为M=1kg的物块静止在桌面边缘,桌面离水平地面的高度为h=1.8m.一质量为m=20g的子弹以水平速度v0=20m/s射入物块,在很短的时间内以水平速度v1=10m/s穿出木块.重力加速度g取10m/s2,求: 如图所示,两个带电荷量分别为q1,q2(q1>q2)的正点电荷,分别固定于真空中的A、B两点,A、B间距离为r.若在它们连线中点O处放置负点电荷Q,则该负点电荷Q受到的库伦力为$\frac{1}{4}$$\frac{KQ}{{r}^{2}}({q}_{1}-{q}_{2})$;若要使Q受到的库伦力为0,则Q应放置在连线上$\frac{\sqrt{K{q}_{1}}}{\sqrt{K{q}_{1}}+\sqrt{K{q}_{2}}}r$处.
如图所示,两个带电荷量分别为q1,q2(q1>q2)的正点电荷,分别固定于真空中的A、B两点,A、B间距离为r.若在它们连线中点O处放置负点电荷Q,则该负点电荷Q受到的库伦力为$\frac{1}{4}$$\frac{KQ}{{r}^{2}}({q}_{1}-{q}_{2})$;若要使Q受到的库伦力为0,则Q应放置在连线上$\frac{\sqrt{K{q}_{1}}}{\sqrt{K{q}_{1}}+\sqrt{K{q}_{2}}}r$处.