题目内容
15.某同学利用下述装置对轻质弹簧的弹性势能进行探究:一轻质弹簧放置在光滑水平桌面上,弹簧左端固定,右端与一小球接触而不固连;弹簧处于原长时,小球恰好在桌面边缘,如图(a)所示.向左推小球,使弹簧压缩一段距离后由静止释放;小球离开桌面后落到水平地面.通过测量和计算,可求得弹簧被压缩后的弹性势能.回答下列问题: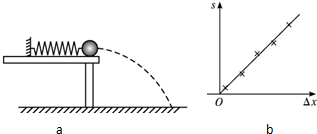
(1)本实验中可认为,弹簧被压缩后的弹性势能Ep与小球抛出时的动能Ek相等.已知重力加速度大小为g.为求得Ek,至少需要测量下列物理量中的ABC(填正确答案标号).
A.小球的质量m B.小球抛出点到落地点的水平距离s
C.桌面到地面的高度h D.弹簧的压缩量△x E.弹簧原长l0
(2)用所选取的测量量和已知量表示Ek,得Ek=$\frac{m{gs}_{\;}^{2}}{4h}$.
(3)图(b)中的直线是实验测量得到的s-△x图线.从理论上可推出,如果 h不变,m增加,s-△x图线的斜率会减小(填“增大”、“减小”或“不变”);如果m不变,h增加,s-△x图线的斜率会增大(填“增大”、“减小”或“不变”).由图(b)中给出的直线关系和Ek的表达式可知,Ep与△x的2次方成正比.
分析 本题的关键是通过测量小球的动能来间接测量弹簧的弹性势能,然后根据平抛规律以及动能表达式即可求出动能的表达式,从而得出结论.本题的难点在于需要知道弹簧弹性势能的表达式(取弹簧因此为零势面),然后再根据${E}_{p}^{\;}$=${E}_{k}^{\;}$即可得出结论.
解答 解:(1)由平抛规律可知,由水平距离和下落高度即可求出平抛时的初速度,进而可求出物体动能,所以本实验至少需要测量小球的质量m、小球抛出点到落地点的水平距离s、桌面到地面的高度h,故选ABC.
(2)由平抛规律应有h=$\frac{1}{2}{gt}_{\;}^{2}$,s=vt,又${E}_{k}^{\;}$=$\frac{1}{2}{mv}_{\;}^{2}$,联立可得${E}_{k}^{\;}$=$\frac{m{gs}_{\;}^{2}}{4h}$
(3)对于确定的弹簧压缩量△x而言,增大小球的质量会减小小球被弹簧加速时的加速度,从而减小小球平抛的初速度和水平位移,即h不变m增加,相同的△x要对应更小的s,s-△x图线的斜率会减小.由s的关系式和s=k△x可知,Ep与△x的二次方成正比.
故答案为:(1)ABC
(2)$\frac{m{gs}_{\;}^{2}}{4h}$
(3)减小,增大,2
点评 本题考查对轻质弹簧的弹性势能进行探究;要注意明确实验原理,根据相应规律得出表达式,然后讨论即可.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
5.两个质量相同的人,分别站在赤道和北纬60°.由于地球自转,那么他们的( )
| A. | 角速度之比为 2:1 | B. | 线速度大小之比为2:1 | ||
| C. | 向心加速度大小之比为4:1 | D. | 向心力大小之比为4:1 |
3. 如图所示,轻杆AB可绕固定轴O转动,A端用轻弹簧连在小车底板上,小车质量为M,B端用细绳拴一小球,小球质量为m.车静止时,AB杆保持水平,当水平外力使小车向左运动时,小球偏离竖直方向且偏角θ逐渐增大,则( )
如图所示,轻杆AB可绕固定轴O转动,A端用轻弹簧连在小车底板上,小车质量为M,B端用细绳拴一小球,小球质量为m.车静止时,AB杆保持水平,当水平外力使小车向左运动时,小球偏离竖直方向且偏角θ逐渐增大,则( )
 如图所示,轻杆AB可绕固定轴O转动,A端用轻弹簧连在小车底板上,小车质量为M,B端用细绳拴一小球,小球质量为m.车静止时,AB杆保持水平,当水平外力使小车向左运动时,小球偏离竖直方向且偏角θ逐渐增大,则( )
如图所示,轻杆AB可绕固定轴O转动,A端用轻弹簧连在小车底板上,小车质量为M,B端用细绳拴一小球,小球质量为m.车静止时,AB杆保持水平,当水平外力使小车向左运动时,小球偏离竖直方向且偏角θ逐渐增大,则( )| A. | 小车做匀加速直线运动 | |
| B. | AB杆仍能保持水平,弹簧弹力不变 | |
| C. | 细绳的张力不变 | |
| D. | 小车受到向右的水平外力大小为(M+m)gtanθ,且逐渐增大 |
10.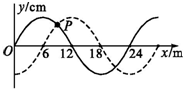 一列水波(横波)沿x轴方向传播,t=0时刻的波形如图中实线所示,t=0.1s(小于一个周期)时刻的波形如图中的虚线所示,下列判断正确的是( )
一列水波(横波)沿x轴方向传播,t=0时刻的波形如图中实线所示,t=0.1s(小于一个周期)时刻的波形如图中的虚线所示,下列判断正确的是( )
 一列水波(横波)沿x轴方向传播,t=0时刻的波形如图中实线所示,t=0.1s(小于一个周期)时刻的波形如图中的虚线所示,下列判断正确的是( )
一列水波(横波)沿x轴方向传播,t=0时刻的波形如图中实线所示,t=0.1s(小于一个周期)时刻的波形如图中的虚线所示,下列判断正确的是( )| A. | 若质点P在t=0时刻向上运动,则水波向右传播 | |
| B. | 质点P的运动方向可能向右 | |
| C. | 水波的传播速度可能为60 m/s | |
| D. | 水波的周期可能为0.6 s |
7. 如图是弹簧振子做简谐振动的装置,其中O为平衡位置,A为弹簧伸得最长的位置,B为弹簧压缩最短的位置,以下说法中正确的是( )
如图是弹簧振子做简谐振动的装置,其中O为平衡位置,A为弹簧伸得最长的位置,B为弹簧压缩最短的位置,以下说法中正确的是( )
 如图是弹簧振子做简谐振动的装置,其中O为平衡位置,A为弹簧伸得最长的位置,B为弹簧压缩最短的位置,以下说法中正确的是( )
如图是弹簧振子做简谐振动的装置,其中O为平衡位置,A为弹簧伸得最长的位置,B为弹簧压缩最短的位置,以下说法中正确的是( )| A. | 振子在O点具有最大加速度和最大位移 | |
| B. | 振子在O点具有最大速度和最大加速度 | |
| C. | 振子在A点具有最大加速度和最大位移 | |
| D. | 振子在B点具有最大速度和最大加速度 |
 如图所示,中间有一个立柱的木箱质量为M,静止于水平桌面上,质量为m的物体中间有孔套在立柱上.m释放后沿立柱匀加速下滑,加速度大小为a(a<g),求此时桌面对木箱的支持力.
如图所示,中间有一个立柱的木箱质量为M,静止于水平桌面上,质量为m的物体中间有孔套在立柱上.m释放后沿立柱匀加速下滑,加速度大小为a(a<g),求此时桌面对木箱的支持力. 质量为m,带电量为q的带电小球,用绝缘细线悬挂在匀强电场中稳定后,细线与竖直方向成θ=45°,如图所示,则该带电小球带正电(填“正”或“负”),受到电场力为mg,电场强度E=$\frac{mg}{q}$.
质量为m,带电量为q的带电小球,用绝缘细线悬挂在匀强电场中稳定后,细线与竖直方向成θ=45°,如图所示,则该带电小球带正电(填“正”或“负”),受到电场力为mg,电场强度E=$\frac{mg}{q}$.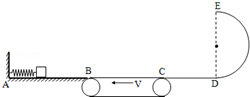 如图所示,光滑水平导轨AB的端有一压缩的弹簧,弹簧左端固定,右端前放一个质量为m=1kg的物块(可视为质点),物块与弹簧不粘连,B点与水平传送带的左端刚好平齐接触,传送带的长度BC的长为L=6m,沿逆时针方向以恒定速度v=2m/s匀速转动.CD为光滑的水平轨道,C点与传送带的右端刚好平齐接触,D是竖直放置的半径为R=0.4m的光滑半圆轨道,DE与CD相切于D点.已知物块与传送带间的动摩擦因数μ=0.2,取g=10m/s2.
如图所示,光滑水平导轨AB的端有一压缩的弹簧,弹簧左端固定,右端前放一个质量为m=1kg的物块(可视为质点),物块与弹簧不粘连,B点与水平传送带的左端刚好平齐接触,传送带的长度BC的长为L=6m,沿逆时针方向以恒定速度v=2m/s匀速转动.CD为光滑的水平轨道,C点与传送带的右端刚好平齐接触,D是竖直放置的半径为R=0.4m的光滑半圆轨道,DE与CD相切于D点.已知物块与传送带间的动摩擦因数μ=0.2,取g=10m/s2.