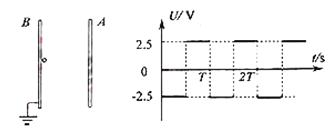
��Ŀ����
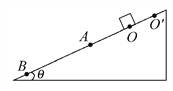
����Ŀ����ͼ��ʾ�������Ϊ����30����б���ϣ��̶�һ��L��0.25 m��ƽ�н������죬�ڵ����϶˽����Դ�ͻ���������R.��Դ�綯��E��12 V������r��1 ����һ����m��20 g�Ľ�����ab�������촹ֱ���Ӵ����ã�����װ�ô��ڴŸ�Ӧǿ��B��0.80 T����ֱ��б�����ϵ���ǿ�ų���(������������ĵ��費��)�����������ǹ⻬�ģ�ȡg��10 m/s2��Ҫ���ֽ������ڵ����Ͼ�ֹ����

��1�����������ܵ��İ������Ĵ�С��
��2��ͨ���������ĵ����Ĵ�С��
��3������������R�����·�е���ֵ��
��4����ͼ�дų�����ֱ����нǻ�����С��00��Ҫ��֤������ʼ�վ�ֹ����B�Ĵ�СӦ��α仯��
���𰸡���1��0.1 N.��2��0.5 A.��3��23 ��.��4��B������
�������������������1���������ܵ��������������͵����֧����������ƽ��״̬������ƽ���������з����������������2����������ų�����ֱ�����ݰ�������ʽF=BIL�������������3������ŷķ�����������������R�����·�е���ֵ����4�����ݶ�̬ƽ������ķ�����������ʸ�������η������жϰ������ı仯��������жϴŸ�Ӧǿ�ȵı仯���.
��1������������������ͼ����ͼ��ʾ
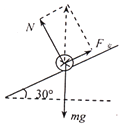
��ƽ�������ã� ![]()
��ã� ![]()
��2�����ݰ�������ʽF=BIL��
![]()
��3��������������·����ֵΪR
���ݱպϵ�·ŷķ![]()
��ã� ![]()
��4����ͼ�дų�����ֱ����нǻ�����С��![]() �����Ÿ�Ӧǿ�ȱ�Ϊ��ֱ���ϣ������������Ϊˮƽ���ң����ڶ�̬ƽ�⣬��ʸ�������η����֪��������С����Ϊ��֧�������䣬�ʰ�������������Ÿ�Ӧǿ��������.
�����Ÿ�Ӧǿ�ȱ�Ϊ��ֱ���ϣ������������Ϊˮƽ���ң����ڶ�̬ƽ�⣬��ʸ�������η����֪��������С����Ϊ��֧�������䣬�ʰ�������������Ÿ�Ӧǿ��������.