题目内容
【题目】如图所示,在竖直平面内的xOy直角坐标系中,以足够长的x轴为水平边界的上方充满方向与x轴的夹角![]() =37°斜向上、电场强度大小为E1(未知)的匀强电场;x轴下方充满正交的匀强电场和匀强磁场,电场的电场强度大小为E2(未知)、方向竖直向上,磁场方向水平向外.一质量为m、电荷量为q的带正电小球(视为质点)从y轴上到原点O距离为L的A点由静止释放,释放后小球沿AP方向做直线运动,从P点进入第IV象限后做匀速圆周运动且恰好经过原点O.已知AP与x轴的夹角也为
=37°斜向上、电场强度大小为E1(未知)的匀强电场;x轴下方充满正交的匀强电场和匀强磁场,电场的电场强度大小为E2(未知)、方向竖直向上,磁场方向水平向外.一质量为m、电荷量为q的带正电小球(视为质点)从y轴上到原点O距离为L的A点由静止释放,释放后小球沿AP方向做直线运动,从P点进入第IV象限后做匀速圆周运动且恰好经过原点O.已知AP与x轴的夹角也为![]() ,取sin37°=0.6,cos37°=0.8,空气阻力不计,重力加速度大小为g.
,取sin37°=0.6,cos37°=0.8,空气阻力不计,重力加速度大小为g.
(1)求小球经过P点时的速度大小v;
(2)求![]() 以及磁场的磁感应强度大小B;
以及磁场的磁感应强度大小B;
(3)若小球从P点进入第IV象限后,立即改变x轴上方的匀强电场,使得小球通过原点O时所受合力与小球速度方向垂直,求改变后的匀强电场的电场强度最小时电场强度的方向和电场强度的最小值Emin以及改变电场后小球第一次经过坐标轴上的位置到P点的距离s.

【答案】(1)![]() (2)
(2)![]() ,
,![]() (3)x轴正方向的夹角为
(3)x轴正方向的夹角为![]() ,
,![]() ,
,![]()
【解析】
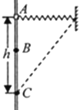
(1)小球从A点运动到原点O过程的受力和运动情况如图甲所示:
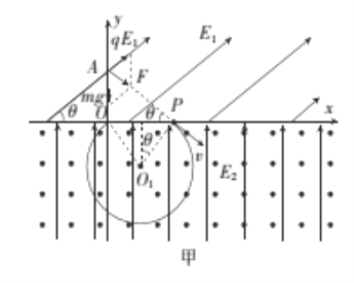
由于小球沿AP方向做直线运动,故该过程小球所受合力F沿AP方向,
根据正弦定理有:
![]()
小球从A点运动到P点的过程中,根据动能定理有:
F·![]()
解得:
v=![]()
(2)根据正弦定理有:
![]()
由于小球从P点进入第IV象限后做匀速圆周运动,有:
qE2=mg
解得:
![]()
由几何关系可得,小球在x轴下方做匀速圆周运动的半径为:
r=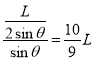
洛伦兹力提供小球做圆周运动所需的向心力,有:
qvB=m![]()
解得:
B=![]()
(3))根据对称性可知,小球经过原点O时的速度方向与x轴正方向的夹角也为![]() (斜向上),如图乙所示,经分析可知,要使小球通过原点O时所受合力方向与速度方向垂直,且改变后的匀强电场的电场强度较小,则此时电场的电场强度方向与x轴正方向的夹角为
(斜向上),如图乙所示,经分析可知,要使小球通过原点O时所受合力方向与速度方向垂直,且改变后的匀强电场的电场强度较小,则此时电场的电场强度方向与x轴正方向的夹角为![]()

根据几何关系有:
![]()
解得:
![]()
小球在第I象限内做类平抛运动的加速度大小为:
a=![]()
经分析可知,改变电场后小球第一次经过的坐标轴为x轴.设小球从原点O到经过x轴的时间为t,改变电场后小球第一次经过轴上的位置到原点O的距离为x1,沿速度方向小球做匀速直线运动,有:
x1cos![]() =vt
=vt
垂直速度方向小球做初速度为零的匀加速直线运动,有:
x1sin![]() =
=![]()
P点到原点O的距离为:
x2=![]()
经分析可知:
s=x1-x2
解得:
s=![]()