Question

如图所示，在E=1×10³N/C的竖直匀强电场中，有一光滑的半圆形绝缘轨道QPN竖直放置与一水平绝缘轨道MN相切连接，P为QN圆弧的中点，其半径R=40cm，一带负电电荷量q=10^-4C的小滑块质量m=20g，与水平轨道间的动摩擦因数μ=0.4，从位于N点右侧s=1.5m处的M点以初速度v₀向左运动，取g=10m/s²．

求：（1）若滑块初速度v₀为6m/s, 则滑块通过P点时对轨道的压力是多大？
（2）若使小滑块在运动中不离开轨道QPN（Q点、N点除外）问小滑块从M点出发时的初速度满足什么条件？

Answer 1

（1）1.3N（2）v₀≥4m/s或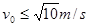

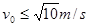
试题分析：（1）设小球到达P点时速度为v， 滑块从开始运动到达P点过程中，由动能定理得-mg?R+qE?R-μ（mg-qE）?S=1/2mv²—1/2 mv₀²         2分
代入数据解得：v²=24m/s             1分
在P点，由支持力提供向心力，由向心力公式N=mv²/ R＝1.3N       2分
由牛顿第三定律得到压力也为1.3N                1分
故运动的滑块通过P点时对轨道的压力是1.3N
（2）设小球恰能到达Q点时速度为v，根据向心力公式，有mg-qE=mv²/ R ，
滑块从开始运动到达Q点过程中，由动能定理得
-mg?2R+qE?2R-μ（mg-qE）?S=1/2mv²—1/2 mv₀²          2分
联立两式并代入数据解得：v₀=4m/s                   1分
若滑块恰能滑到P点停止，滑块从开始运动到达P点过程中，由动能定理有
qE?R-mg?R-μ（mg-qE）?S="0—1/2" mv₀²             2分
代入数据解得：v₀²=10m/s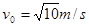，1分
综上所述，小滑块在运动中不离开轨道，小滑块从M点出发时的初速度必须满足：v₀≥4m/s或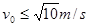2分
点评：在应用动能定理求解问题时，要明确两个状态一个过程，要进行受力分析和做功分析，本题又考查了圆周运动的知识，可见是一个综合性比较强的题目