题目内容
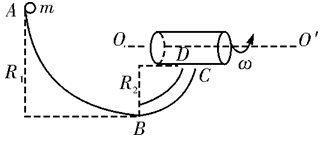
(9分)如图所示,竖直固定放置的斜面AB的下端与光滑的圆弧轨道BCD的B端相切,圆弧面的半径为R,圆心O与A、D在同一水平面上,∠COB=θ,现有一质量为m的小物体从斜面上的A点无初速滑下,已知小物体与AB斜面间的动摩擦因数为μ,重力加速度为g。求:
(1)小物体在斜面上能够通过的路程;
(2)小物体通过C点时,对C点的最大压力和最小压力。
(1)小物体在斜面上能够通过的路程;
(2)小物体通过C点时,对C点的最大压力和最小压力。

(1)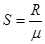 (2)
(2)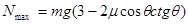 ,
,
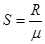 (2)
(2)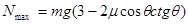 ,
,
本题考查动能定理的应用,动能定理适用于直线运动或曲线运动,克服摩擦力做功与路径有关,W=fs其中的s应为路程
(1)小物体最终将在以过圆心的半径两侧q范围内运动,由动能定理得
μmgcosθ -fs =0 ............2分
又 f=μmgcosθ ............1分
解得 :S=μ/m ............2分
(2)小物体第一次到达最低点时对C点的压力;
 ............1分
............1分
由动能定理得: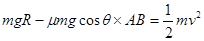 ............2分
............2分
AB=Rcotθ
解得:Nm=mg(3-2µcosqcotθ) ............1分
(2) 当小物体最后在BCD/(D/在C点左侧与B等高)圆弧上运动时,通过C点时对轨道压力最小。
Nn-mg=m(v/)2/R, ............1分
mgR(1-cosθ)=m(v/)2/2 ............2分
解得:N n=" mg" (3-2cosθ). ............1分
(1)小物体最终将在以过圆心的半径两侧q范围内运动,由动能定理得
μmgcosθ -fs =0 ............2分
又 f=μmgcosθ ............1分
解得 :S=μ/m ............2分
(2)小物体第一次到达最低点时对C点的压力;
 ............1分
............1分由动能定理得:
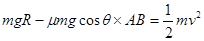 ............2分
............2分AB=Rcotθ
解得:Nm=mg(3-2µcosqcotθ) ............1分
(2) 当小物体最后在BCD/(D/在C点左侧与B等高)圆弧上运动时,通过C点时对轨道压力最小。
Nn-mg=m(v/)2/R, ............1分
mgR(1-cosθ)=m(v/)2/2 ............2分
解得:N n=" mg" (3-2cosθ). ............1分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目




 r,图6甲所示为立体图,图6乙所示为侧视图.现将两杆沿水平方向缓慢靠近直至两杆接触为止,在此过程中 ( )
r,图6甲所示为立体图,图6乙所示为侧视图.现将两杆沿水平方向缓慢靠近直至两杆接触为止,在此过程中 ( )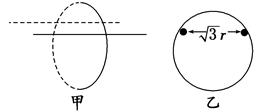
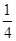 mgr
mgr