题目内容
如图，在光滑水平面上停放着质量为m的装有光滑弧形槽的小车，一质量也为m的小球以水平初速度v
0沿槽口向小车滑去，到达某一高度后，小球又返回右端，则（ ）
|
|
|
|
分析：选取小球与小车组成的系统为研究对象，系统整个过程水平方向动量守恒，竖直方向动量不守恒，系统的机械能守恒，所以相当于弹性碰撞！
当铁块回到小车右端时，铁块的速度为0，小车具有向左的速度．当小球与小车的水平速度相等时，小球弧形槽上升到最大高度．
解答：解：A、系统整个过程水平方向动量守恒，竖直方向动量不守恒，故A错误；
B、设小球离开小车时，小球的速度为v
1，小车的速度为v
2，整个过程中动量守恒，得：
mv
0=mv
1+mv
2 ①
由动能守恒得：
m=m+m ②
联立①②，解得：v
1=0，v
2=v
0，即小球与小车分离后二者交换速度；所以小球与小车分离后做自由落体运动．故B错误；
C、此过程中小球对小车的功等于小车动能的增加，即
W=△Ek=m．故C正确；
D、当小球与小车的水平速度相等时，小球弧形槽上升到最大高度，设该高度为h，则：mv
0=2m?v ③
m=?2mv2+mgh ④
联立③④解得：
h=．故D正确．
故选：CD
点评：解决本题关键是能够把动量守恒，结合机械能守恒．抓住当小球与小车的水平速度相等时，小球弧形槽上升到最大高度．
练习册系列答案
相关题目
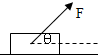如图，在光滑水平面上有一质量为m的物体，在与水平方向成θ角的恒定拉力F作用下运动，则在时间t内（ ）
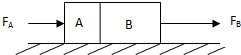如图，在光滑水平面上放着紧靠在一起的A、B两物体，B的质量是A的2倍，B受到向右的恒力FB=2N，A受到的水平力FA=（9-2t）N（t的单位是s），从t=0开始计时，则下列说法不正确的是（ ）
如图，在光滑水平面上放着质量分别为m和2m的A、B两个物块，现用外力缓慢向左推B使弹簧压缩，此过程中推力做功W．然后撤去外力，则（ ）
如图，在光滑水平面上，有一竖直向下的匀强磁场，分布在宽度为L的区域内，现有一边长为l（l＜L）的正方形闭合导线框以垂直磁场边界的初速度v1滑进磁场，然后线圈滑出磁场的速度为v2，设线框滑进磁场的时间为t1，安接力的冲量为I1，线框产生的热量为Q1，线框滑出磁场的时间为t2，安培力的冲量为I2，线框产生的热量为Q2，则有（ ）