题目内容
 如图,在光滑水平面上,有一竖直向下的匀强磁场,分布在宽度为L的区域内,现有一边长为l(l<L)的正方形闭合导线框以垂直磁场边界的初速度v1滑进磁场,然后线圈滑出磁场的速度为v2,设线框滑进磁场的时间为t1,安接力的冲量为I1,线框产生的热量为Q1,线框滑出磁场的时间为t2,安培力的冲量为I2,线框产生的热量为Q2,则有( )
如图,在光滑水平面上,有一竖直向下的匀强磁场,分布在宽度为L的区域内,现有一边长为l(l<L)的正方形闭合导线框以垂直磁场边界的初速度v1滑进磁场,然后线圈滑出磁场的速度为v2,设线框滑进磁场的时间为t1,安接力的冲量为I1,线框产生的热量为Q1,线框滑出磁场的时间为t2,安培力的冲量为I2,线框产生的热量为Q2,则有( )分析:两个过程线框磁通量变化量大小大小相等,则两个过程电量相等.联立就可求出完全进入磁场中时线圈的速度.根据能量守恒表示出两次过程产生的热量然后结合数学知识进行比较.
解答:解:A、磁场进入或穿出磁场的过程产生感应电流,受到向左的安培力,线框会减速,故v1>v2,故A错误;
B、线框到达右边界的初速度等于从左边界完全进入后的末速度,故穿出右边界时的速度小于穿过左边界的速度,t=
,则t1<t2,故B正确;
C、对线框进入或穿出磁场过程,设初速度为v,末速度为v′.由动量定理可知:B
L△t=mv′-mv,又电量q=I△t,得:m(v′-v)=BLq,
得:速度变化量△v=v′-v=
由q=
可知,进入和穿出磁场过程,磁通量的变化量相等,则进入和穿出磁场的两个过程通过导线框横截面积的电量相等,故安培力的冲量I1=I2,故C正确;
D、进入过程导线框的速度变化量等于离开过程导线框的速度变化量.
设开始进入磁场时速度为v1,完全进入磁场中时,线圈的速度大小为v′,完全穿出磁场后速度为v2,则有:
v1-v′=v′-v2,
根据能量守恒:Q1=
mv12-
mv′2=
m(v1+v′)(v1-v′)
Q2=
v′2-
mv22=
m(v′+v2)(v′-v2)
由前面分析知:v1+v′>v′+v2故Q1>Q2,故D正确;
故选:BCD.
B、线框到达右边界的初速度等于从左边界完全进入后的末速度,故穿出右边界时的速度小于穿过左边界的速度,t=
| l |
| v |
C、对线框进入或穿出磁场过程,设初速度为v,末速度为v′.由动量定理可知:B
. |
| I |
得:速度变化量△v=v′-v=
| BLq |
| m |
由q=
| n△Φ |
| R |
D、进入过程导线框的速度变化量等于离开过程导线框的速度变化量.
设开始进入磁场时速度为v1,完全进入磁场中时,线圈的速度大小为v′,完全穿出磁场后速度为v2,则有:
v1-v′=v′-v2,
根据能量守恒:Q1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
Q2=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
由前面分析知:v1+v′>v′+v2故Q1>Q2,故D正确;
故选:BCD.
点评:根据动量定理求解电量或速度的变化是常用的方法,还要掌握电磁感应中能量问题的求解,是考试的热点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
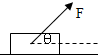 如图,在光滑水平面上有一质量为m的物体,在与水平方向成θ角的恒定拉力F作用下运动,则在时间t内( )
如图,在光滑水平面上有一质量为m的物体,在与水平方向成θ角的恒定拉力F作用下运动,则在时间t内( )| A、重力的冲量为0 | B、拉力F的冲量为Ft | C、拉力F的冲量为Ftcosθ | D、拉力F的冲量等于物体动量的变化量 |
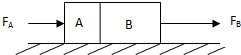 如图,在光滑水平面上放着紧靠在一起的A、B两物体,B的质量是A的2倍,B受到向右的恒力FB=2N,A受到的水平力FA=(9-2t)N(t的单位是s),从t=0开始计时,则下列说法不正确的是( )
如图,在光滑水平面上放着紧靠在一起的A、B两物体,B的质量是A的2倍,B受到向右的恒力FB=2N,A受到的水平力FA=(9-2t)N(t的单位是s),从t=0开始计时,则下列说法不正确的是( ) 如图,在光滑水平面上放着质量分别为m和2m的A、B两个物块,现用外力缓慢向左推B使弹簧压缩,此过程中推力做功W.然后撤去外力,则( )
如图,在光滑水平面上放着质量分别为m和2m的A、B两个物块,现用外力缓慢向左推B使弹簧压缩,此过程中推力做功W.然后撤去外力,则( )