题目内容
20.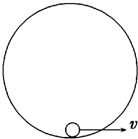 如图所示,一个质量为m的小球在半径为R的光滑竖直圆轨道内做圆周运动,当小球从圆的最低点以速度v=$\sqrt{5Rg}$出发,则下列判断正确的是(重力加速度为g)( )
如图所示,一个质量为m的小球在半径为R的光滑竖直圆轨道内做圆周运动,当小球从圆的最低点以速度v=$\sqrt{5Rg}$出发,则下列判断正确的是(重力加速度为g)( )| A. | 不能通过最高点 | |
| B. | 再次通过圆的最低点时,小球对轨道的压力为6mg | |
| C. | 通过最高点时,圆对小球的弹力为mg | |
| D. | 通过最高点时,圆对小球的弹力为0 |
分析 根据动能定理列式求解最高点的速度,根据最小速度进行比较,看能否通过最高点,根据牛顿第二定律列式分别求解最高点和最低点的弹力.
解答 解:A、从最低点到最高点的过程中,根据动能定理得:
$\frac{1}{2}m{{v}_{1}}^{2}-\frac{1}{2}m{v}^{2}=-mg•2R$
解得:${v}_{1}=\sqrt{gR}$,所以小球恰好通过最高点,故A错误;
B、再次通过圆的最低点时速度仍为v=$\sqrt{5Rg}$,根据牛顿第二定律得:
${F}_{N1}-mg=m\frac{{v}^{2}}{R}$
解得:FN1=5mg+mg=6mg,
根据牛顿第三定律可知,小球对轨道的压力为6mg,故B正确;
C、在最高点,根据牛顿第二定律得:
${F}_{N}+mg=m\frac{{{v}_{1}}^{2}}{R}$
解得:FN=0,故C错误,D正确.
故选:BD
点评 本题是竖直平面内的圆周运动问题;在最高点和最低点,合力提供向心力;同时整个过程机械能守恒,难度适中.

练习册系列答案
相关题目
8.下列关于加速度和速度的描述中,正确的是( )
| A. | 加速度在数值上等于单位时间里速度的变化量 | |
| B. | 当加速度与速度方向相同且又减小时,物体做减速运动 | |
| C. | 加速度方向一定和速度方向相同 | |
| D. | 速度变化越来越快,加速度越来越小 |
5.两根完全相同的金属丝甲和乙,长度均为L,横截面积均为S,将乙拉长为原来的两倍后,将两根金属丝串联在同一电路中,甲、乙金属丝两端的电压之比为( )
| A. | 1:2 | B. | 2:1 | C. | 1:4 | D. | 4:1 |
10.要使真空中的两个点电荷间的库仑力增大到原来的4倍,下列方法可行的是( )
| A. | 每个点电荷的电荷量都增大到原来的2倍,电荷间的距离变为原来的$\frac{1}{2}$ | |
| B. | 保持点电荷的电荷量不变,使两个点电荷的距离增大到原来的2倍 | |
| C. | 使一个点电荷的电荷量增加1倍,另一个点电荷的电荷量保持不变,同时使两点电荷间的距离减小为原来的$\frac{1}{2}$ | |
| D. | 保持点电荷的电荷量不变,将两点电荷间的距离减小为原来的$\frac{1}{2}$ |
 某同学想在家里做“用单摆测定重力加速度”的实验,但没有合适的摆球,他找到了一块大小约为3cm、外形不规则的大理石代替小球.他设计的实验步骤如下:
某同学想在家里做“用单摆测定重力加速度”的实验,但没有合适的摆球,他找到了一块大小约为3cm、外形不规则的大理石代替小球.他设计的实验步骤如下:
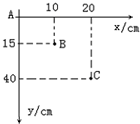 在“研究平抛运动”实验中,某同学只记录了小球运动途中的A、B、C三点的位置,取A点为坐标原点,则各点的位置坐标如图所示,g取10m/s2,则:
在“研究平抛运动”实验中,某同学只记录了小球运动途中的A、B、C三点的位置,取A点为坐标原点,则各点的位置坐标如图所示,g取10m/s2,则: 如图所示,水平放置的两平行金属板A、B接在U=4 000V的直流电源上,两极板间距离为2cm,A极板接地,电场中a点距B极板1cm,b点和c点均距A极板0.5cm,求:
如图所示,水平放置的两平行金属板A、B接在U=4 000V的直流电源上,两极板间距离为2cm,A极板接地,电场中a点距B极板1cm,b点和c点均距A极板0.5cm,求: 如图是一种清洗车辆用的手持式喷水枪.设枪口的截面积为0.6cm2,要有效清洗车辆,喷出的水的速度至少为20m/s,(水的密度为1×103kg/m3).试估计水枪工作时的功率至少为多大?
如图是一种清洗车辆用的手持式喷水枪.设枪口的截面积为0.6cm2,要有效清洗车辆,喷出的水的速度至少为20m/s,(水的密度为1×103kg/m3).试估计水枪工作时的功率至少为多大?