题目内容
15.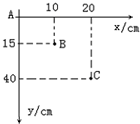 在“研究平抛运动”实验中,某同学只记录了小球运动途中的A、B、C三点的位置,取A点为坐标原点,则各点的位置坐标如图所示,g取10m/s2,则:
在“研究平抛运动”实验中,某同学只记录了小球运动途中的A、B、C三点的位置,取A点为坐标原点,则各点的位置坐标如图所示,g取10m/s2,则:(1)平抛的初速度为1m/s.
(2)小球抛出点的位置坐标是(-10cm,-5cm).
(3)小球经过C点时的速度为$\sqrt{10}$m/s.
分析 平抛运动在竖直方向上做自由落体运动,根据△y=gT2求出相邻两点的时间间隔,根据水平方向上的匀速直线运动求出平抛运动的初速度.求出B点在竖直方向上的分速度,根据vy=gt求出运动到B点的时间,得出水平位移和竖直位移,从而求出抛出点的位置坐标.
解答 解:根据△y=gT2得
T=$\sqrt{\frac{△y}{g}}$=$\sqrt{\frac{0.4-0.15-0.15}{10}}$=0.1s
则平抛运动的初速度v0=$\frac{x}{T}$=$\frac{0.1}{0.1}$=1m/s
那么小球运动到B点的时间t=$\frac{{v}_{y}}{g}$=$\frac{2}{10}$=0.2s
所以B点的水平位移x=v0t=0.2m=20cm,
竖直位移y=$\frac{1}{2}$gt2=$\frac{1}{2}$×10×0.04=20cm
所以小球抛出点的位置横坐标为10-20cm=-10cm,
纵坐标为15-20cm=-5cm.
所以小球抛出点的位置坐标为(-10cm,-5cm).
B点竖直方向上的分速度vy=$\frac{{y}_{AC}}{2T}$=$\frac{0.4}{0.2}$=2m/s
那么C点竖直方向上的分速度为vy′=2+10×0.1=3m/s
则C点的速度vC=$\sqrt{{v}_{0}^{2}+{v}_{y}^{2}}$=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$ m/s
故答案为:1,-10,-5,$\sqrt{10}$.
点评 解决本题的关键掌握平抛运动水平方向和竖直方向上的运动规律,灵活运用运动学公式进行求解.

练习册系列答案
相关题目
3.以下说法正确的是( )
| A. | X射线是处于激发态的原子核辐射出的 | |
| B. | 比结合能越大,表示原子核中核子结合得越牢靠,原子核越稳定 | |
| C. | 放射性元素发生一次β衰变,原子序数增加1 | |
| D. | 当氢原子从n=3的状态跃迁到n=2的状态时,核外电子的运动加速度减小 |
10.旺苍东城中学正在举行班级对抗赛,张明明同学是短跑运动员,在百米竞赛中,测得他在6s末的速度为9.5m/s,12.5s末到达终点的速度为9.8m/s,则他在全程中的平均速度为( )
| A. | 9.5 m/s | B. | 9.8 m/s | C. | 10.m/s | D. | 8.0m/s |
20.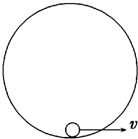 如图所示,一个质量为m的小球在半径为R的光滑竖直圆轨道内做圆周运动,当小球从圆的最低点以速度v=$\sqrt{5Rg}$出发,则下列判断正确的是(重力加速度为g)( )
如图所示,一个质量为m的小球在半径为R的光滑竖直圆轨道内做圆周运动,当小球从圆的最低点以速度v=$\sqrt{5Rg}$出发,则下列判断正确的是(重力加速度为g)( )
 如图所示,一个质量为m的小球在半径为R的光滑竖直圆轨道内做圆周运动,当小球从圆的最低点以速度v=$\sqrt{5Rg}$出发,则下列判断正确的是(重力加速度为g)( )
如图所示,一个质量为m的小球在半径为R的光滑竖直圆轨道内做圆周运动,当小球从圆的最低点以速度v=$\sqrt{5Rg}$出发,则下列判断正确的是(重力加速度为g)( )| A. | 不能通过最高点 | |
| B. | 再次通过圆的最低点时,小球对轨道的压力为6mg | |
| C. | 通过最高点时,圆对小球的弹力为mg | |
| D. | 通过最高点时,圆对小球的弹力为0 |
4.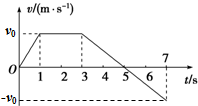 物体沿直线运动的v-t关系图象如图所示,已知在第1秒内合外力对物体所做的功为W,则( )
物体沿直线运动的v-t关系图象如图所示,已知在第1秒内合外力对物体所做的功为W,则( )
 物体沿直线运动的v-t关系图象如图所示,已知在第1秒内合外力对物体所做的功为W,则( )
物体沿直线运动的v-t关系图象如图所示,已知在第1秒内合外力对物体所做的功为W,则( )| A. | 从第1秒末到第3秒末合外力做功为W | |
| B. | 从第3秒末到第5秒末合外力做功为-2W | |
| C. | 从第5秒末到第7秒末合外力做功为-W | |
| D. | 从第3秒末到第4秒末合外力做功为-0.75W |

