题目内容
20.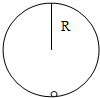 如图,光滑的竖直圆轨道半径为R,一个小球在其内侧运动.已知小球恰好通过轨道的最高点,若重力加速度为g,
如图,光滑的竖直圆轨道半径为R,一个小球在其内侧运动.已知小球恰好通过轨道的最高点,若重力加速度为g,试求 ①小球通过最高点的速度v
②小球通过最低点的速度v0.
分析 小球恰好通过轨道的最高点,可知轨道对小球的弹力为零,靠重力提供向心力,根据牛顿第二定律求出最高点的速度.根据动能定理求出小球通过最低点的速度.
解答 解:①根据牛顿第二定律得,mg=$m\frac{{v}^{2}}{R}$,
解得v=$\sqrt{gR}$.
②根据动能定理得,$mg•2R=\frac{1}{2}m{{v}_{0}}^{2}-\frac{1}{2}m{v}^{2}$,
解得v0=$\sqrt{5gR}$.
答:①小球通过最高点的速度v为$\sqrt{gR}$;
②小球通过最低点的速度v0为$\sqrt{5gR}$.
点评 本题考查了圆周运动的基本运用,知道最高点向心力来源,以及知道最高点的临界情况,结合牛顿第二定律进行求解,基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.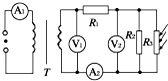 如图所示,T为理想变压器,原副线圈匝数比为5:1.A1、A2为理想交流电流表,V1、V2为理想交流电压表,R1、R2为定值电阻,R3为光敏电阻(阻值随光照强度的增大而减小),原线圈两端电压u=220$\sqrt{2}$sin314tV,以下说法正确的是( )
如图所示,T为理想变压器,原副线圈匝数比为5:1.A1、A2为理想交流电流表,V1、V2为理想交流电压表,R1、R2为定值电阻,R3为光敏电阻(阻值随光照强度的增大而减小),原线圈两端电压u=220$\sqrt{2}$sin314tV,以下说法正确的是( )
 如图所示,T为理想变压器,原副线圈匝数比为5:1.A1、A2为理想交流电流表,V1、V2为理想交流电压表,R1、R2为定值电阻,R3为光敏电阻(阻值随光照强度的增大而减小),原线圈两端电压u=220$\sqrt{2}$sin314tV,以下说法正确的是( )
如图所示,T为理想变压器,原副线圈匝数比为5:1.A1、A2为理想交流电流表,V1、V2为理想交流电压表,R1、R2为定值电阻,R3为光敏电阻(阻值随光照强度的增大而减小),原线圈两端电压u=220$\sqrt{2}$sin314tV,以下说法正确的是( )| A. | 当光照增强时,电压表V1示数为44$\sqrt{2}$V保持不变 | |
| B. | 当光照增强时,电压表V2示数变大 | |
| C. | 通过电流表A1的电流方向每秒变化50次 | |
| D. | 当光照增强时,电流表A1、A2示数同时变大 |
5.把一电热器接到110V的直流电源上,在时间t内产生热量为Q.若将它接到电压为u=110sin100πt(V)的交流电上,要产生热量为2Q,则所需的通电时间为( )
| A. | 4t | B. | $\sqrt{2}$t | C. | 2t | D. | t |
10.如图所示,为一列横波t=0时刻波的图象,并向右传播,经过1.1秒,质点A第三次处于波峰,则则下列说法正确的是( )
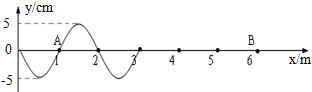

| A. | 这列波的波速为5m/s | B. | 这列波的波速为4m/s | ||
| C. | 经过0.5s质点B第一次到达波峰 | D. | 经过0.9s质点B第一次到达波峰 |
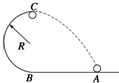 如图所示,小球在外力作用下,由静止开始从A点出发做匀加速直线运动,到B点时撤去外力,小球冲上竖直平面内半径为R的光滑半圆轨道.
如图所示,小球在外力作用下,由静止开始从A点出发做匀加速直线运动,到B点时撤去外力,小球冲上竖直平面内半径为R的光滑半圆轨道. 体育老师在操场司令台上将哨子以8m/s的速度水平抛出,经过0.6s后落地,若不计空气阻力,求:
体育老师在操场司令台上将哨子以8m/s的速度水平抛出,经过0.6s后落地,若不计空气阻力,求: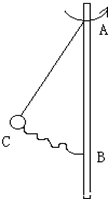 如图所示,小球质量m=0.8kg,用两根长L=0.5m长的细绳拴住并系在竖直杆上的A、B两点,AB=0.8m,直杆转动带动小球在水平面内做圆周运动,当绕杆以ω=40rad/s的角速度匀速转动时,求上下两根绳上的张力(g=10m/s2)
如图所示,小球质量m=0.8kg,用两根长L=0.5m长的细绳拴住并系在竖直杆上的A、B两点,AB=0.8m,直杆转动带动小球在水平面内做圆周运动,当绕杆以ω=40rad/s的角速度匀速转动时,求上下两根绳上的张力(g=10m/s2)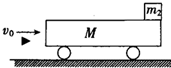 如图所示,一质量M=0.25kg的平顶小车,车顶右端放一质量m2=0.2kg的小物体,小物体可视为质点,与车顶之间的动摩擦因数μ=0.4,小车静止在光滑的水平轨道上.现有一质量m1=0.05kg的子弹以水平速度v0=12m/s射中小车左端,并留在车中,子弹与车相互作用时间很短.若使小物体不从车顶上滑落,
如图所示,一质量M=0.25kg的平顶小车,车顶右端放一质量m2=0.2kg的小物体,小物体可视为质点,与车顶之间的动摩擦因数μ=0.4,小车静止在光滑的水平轨道上.现有一质量m1=0.05kg的子弹以水平速度v0=12m/s射中小车左端,并留在车中,子弹与车相互作用时间很短.若使小物体不从车顶上滑落,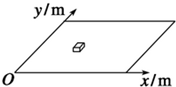 在研究某些曲线运动时,可将曲线运动分解为几个独立的直线运动处理,如:匀速直线运动、匀变速直线运动等.如图所示,一物体在水平外力的作用下沿水平面(xoy平面)运动,已知物体运动过程中的坐标与时间的关系为$\left\{\begin{array}{l}{x=1.5t}\\{y=2t-2{t}^{2}}\end{array}\right.$,g=10 m/s2.根据以上条件,求:
在研究某些曲线运动时,可将曲线运动分解为几个独立的直线运动处理,如:匀速直线运动、匀变速直线运动等.如图所示,一物体在水平外力的作用下沿水平面(xoy平面)运动,已知物体运动过程中的坐标与时间的关系为$\left\{\begin{array}{l}{x=1.5t}\\{y=2t-2{t}^{2}}\end{array}\right.$,g=10 m/s2.根据以上条件,求: