题目内容
9.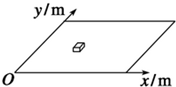 在研究某些曲线运动时,可将曲线运动分解为几个独立的直线运动处理,如:匀速直线运动、匀变速直线运动等.如图所示,一物体在水平外力的作用下沿水平面(xoy平面)运动,已知物体运动过程中的坐标与时间的关系为$\left\{\begin{array}{l}{x=1.5t}\\{y=2t-2{t}^{2}}\end{array}\right.$,g=10 m/s2.根据以上条件,求:
在研究某些曲线运动时,可将曲线运动分解为几个独立的直线运动处理,如:匀速直线运动、匀变速直线运动等.如图所示,一物体在水平外力的作用下沿水平面(xoy平面)运动,已知物体运动过程中的坐标与时间的关系为$\left\{\begin{array}{l}{x=1.5t}\\{y=2t-2{t}^{2}}\end{array}\right.$,g=10 m/s2.根据以上条件,求:(1)物体运动的加速度大小;
(2)经t=1s时物体的速度大小;
(3)经t=2s时物体的位移大小.
分析 由坐标与时间的关系为$\left\{\begin{array}{l}{x=1.5t}\\{y=2t-2{t}^{2}}\end{array}\right.$,可知,两方向的运动性质,再根据牛顿第二定律求加速度;及运动学公式求t=1s时物体的速度和t=2s时物体的位移大小.
解答 解:(1)物体运动过程中的坐标与时间的关系为$\left\{\begin{array}{l}{x=1.5t}\\{y=2t-2{t}^{2}}\end{array}\right.$,
x方向以速度1.5m/s做匀速直线运动;而y方向以初速度为2m/s,加速度为-4m/s2,做匀变速直线运动,
根据运动的合成可知,物体的加速度为:a=4m/s2
(2)t=1s时,x方向的速度为vx=1.5m/s;
而y方向的速度:vy=v0+at=2-4×1=-2m/s
根据矢量的合成法则,则t=1s时物体的速度大小v=$\sqrt{{v}_{x}^{2}+{v}_{y}^{2}}$=$\sqrt{1.{5}^{2}+{2}^{2}}$=2.5m/s;
(3)t=2s时,x方向的位移为sx=1.5×2=3m;
而y方向的位移为sy=v0t+$\frac{1}{2}$at2=2×2-$\frac{1}{2}×4×{2}^{2}$=-4m;
因此2s时物体的位移大小s=$\sqrt{{3}^{2}+{4}^{2}}$=5m
答:(1)物体的加速度大小为4m/s2;
(2)t=1s时物体的速度大小为2.5m/s;
(3)t=2s时物体发生的位移大小5m.
点评 本题考查牛顿第二定律和运动学公式,加速度是将力与运动联系起来的桥梁,注意运动学公式中加速度的正负值.

练习册系列答案
相关题目
17.(多选)以下说法正确的是( )
| A. | 在“用单摆测定重力加速度”实验中,为了减小实验误差应从摆动的最低点开始计时 | |
| B. | 不同颜色的光在真空中的速度都是相同的 | |
| C. | 两列波相叠加产生干涉现象,振动加强区域与减弱区域应交替变化 | |
| D. | LC回路中的振荡电流为零时,电容器极板间的场强最大 |
4.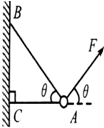 如图所示,物体的质量为2kg,两根轻细绳AB和AC的一端固定于竖直墙上,另一端系于物体上(∠BAC=θ=60°),在物体上另施加一个方向与水平线也成θ角的拉力F,若要使绳都能伸直,下列F中不可能的是(取g=10m/s2)( )
如图所示,物体的质量为2kg,两根轻细绳AB和AC的一端固定于竖直墙上,另一端系于物体上(∠BAC=θ=60°),在物体上另施加一个方向与水平线也成θ角的拉力F,若要使绳都能伸直,下列F中不可能的是(取g=10m/s2)( )
 如图所示,物体的质量为2kg,两根轻细绳AB和AC的一端固定于竖直墙上,另一端系于物体上(∠BAC=θ=60°),在物体上另施加一个方向与水平线也成θ角的拉力F,若要使绳都能伸直,下列F中不可能的是(取g=10m/s2)( )
如图所示,物体的质量为2kg,两根轻细绳AB和AC的一端固定于竖直墙上,另一端系于物体上(∠BAC=θ=60°),在物体上另施加一个方向与水平线也成θ角的拉力F,若要使绳都能伸直,下列F中不可能的是(取g=10m/s2)( )| A. | 4$\sqrt{3}$N | B. | 8$\sqrt{3}$N | C. | 12$\sqrt{3}$N | D. | 16$\sqrt{3}$N |
14.关于光的本性,下列描述不正确的是( )
| A. | 泊松亮斑说明光具有波动性 | B. | 薄膜干涉说明光具有波动性 | ||
| C. | 单缝衍射说明光具有波动性 | D. | 偏振现象说明光是一种纵波 |
1.做“研究平抛运动”的实验时,让小球多次沿同一轨道运动,通过描点法画小球做平抛运动的轨迹,为了能准确地描绘运动轨迹,下面列出了一些操作要求,你认为不正确的是( )
| A. | 通过调节使斜槽的末端保持水平 | |
| B. | 每次释放小球的位置可以不同 | |
| C. | 每次必须由静止释放小球 | |
| D. | 小球运动时不应与木板上的白纸(或方格纸)相接触 |
18.根据表格中的内容,判断下列说法正确的是( )
| 材料 | 铯 | 钙 | 镁 | 铍 | 钛 | 金 |
| 逸出功W/eV | 1.9 | 2.7 | 3.7 | 3.9 | 4.1 | 4.8 |
| A. | 只要入射光的强度足够大,照射时间足够长,表中的金属均可以发生光电效应 | |
| B. | 用某光照射表中金属,均能够发生光电效应,则从铯表面逸出的光电子的最大初动能最大 | |
| C. | 使表中金属发生光电效应时,金的极限频率最小 | |
| D. | 使表中金属发生光电效应时,铯的极限频率最小 | |
| E. | 使表中金属发生光电效应时,金的极限波长最小 |
19.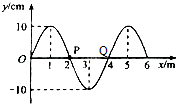 一列简谐横波在t=0时的波形图如图所示.介质中x=2m处的质点P沿y轴方向做简谐运动的表达式为y=10sin(5πt)cm.质点Q的平衡位置在x=4m处,关于这列简谐波,下列说法正确的是( )
一列简谐横波在t=0时的波形图如图所示.介质中x=2m处的质点P沿y轴方向做简谐运动的表达式为y=10sin(5πt)cm.质点Q的平衡位置在x=4m处,关于这列简谐波,下列说法正确的是( )
 一列简谐横波在t=0时的波形图如图所示.介质中x=2m处的质点P沿y轴方向做简谐运动的表达式为y=10sin(5πt)cm.质点Q的平衡位置在x=4m处,关于这列简谐波,下列说法正确的是( )
一列简谐横波在t=0时的波形图如图所示.介质中x=2m处的质点P沿y轴方向做简谐运动的表达式为y=10sin(5πt)cm.质点Q的平衡位置在x=4m处,关于这列简谐波,下列说法正确的是( )| A. | 周期为0.4s | B. | 传播速度为5m/s | ||
| C. | 传播方向沿x轴负向 | D. | 质点P与质点Q的速度方向总是相反 |

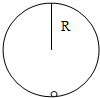 如图,光滑的竖直圆轨道半径为R,一个小球在其内侧运动.已知小球恰好通过轨道的最高点,若重力加速度为g,
如图,光滑的竖直圆轨道半径为R,一个小球在其内侧运动.已知小球恰好通过轨道的最高点,若重力加速度为g,