题目内容
12.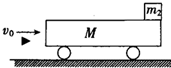 如图所示,一质量M=0.25kg的平顶小车,车顶右端放一质量m2=0.2kg的小物体,小物体可视为质点,与车顶之间的动摩擦因数μ=0.4,小车静止在光滑的水平轨道上.现有一质量m1=0.05kg的子弹以水平速度v0=12m/s射中小车左端,并留在车中,子弹与车相互作用时间很短.若使小物体不从车顶上滑落,
如图所示,一质量M=0.25kg的平顶小车,车顶右端放一质量m2=0.2kg的小物体,小物体可视为质点,与车顶之间的动摩擦因数μ=0.4,小车静止在光滑的水平轨道上.现有一质量m1=0.05kg的子弹以水平速度v0=12m/s射中小车左端,并留在车中,子弹与车相互作用时间很短.若使小物体不从车顶上滑落,求:(1)小车的最短长度为多少?
(2)最后小物体与车的共同速度为多少?
分析 子弹射入小车的过程动量守恒,根据动量守恒定律列式,物块在小车上向左滑行的过程,两者的总动量守恒,总能量守恒,根据动量守恒定律以及能量守恒定律列式,联立方程即可求得小车与物块保持相对静止的速度和小车的最短长度.
解答 解:子弹射入小车的过程,设向右为正方向,根据动量守恒:m1 v0=( M+m1 ) v1
小车与与木块向左作用的过程动量守恒:( M+m1 ) v1=( M+m1+m2) v2
根据功能关系:$\frac{1}{2}$( M+m1 ) v12-$\frac{1}{2}$( M+m1+m2) v22=μm2gL
联立并代入数据得车长为::L=0.3m
共同速度:v2=1.2m/s
答:(1)小车的最短长度为0.3m;
(2)最后小物体与车的共同速度为1.2m/s.
点评 本题主要考查了动量守恒定律、能量守恒定律的直接应用,关键是知道在子弹射入小车的过程动量守恒,子弹射入小车的过程动量守恒,难度适中.

练习册系列答案
相关题目
17.(多选)以下说法正确的是( )
| A. | 在“用单摆测定重力加速度”实验中,为了减小实验误差应从摆动的最低点开始计时 | |
| B. | 不同颜色的光在真空中的速度都是相同的 | |
| C. | 两列波相叠加产生干涉现象,振动加强区域与减弱区域应交替变化 | |
| D. | LC回路中的振荡电流为零时,电容器极板间的场强最大 |
4.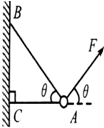 如图所示,物体的质量为2kg,两根轻细绳AB和AC的一端固定于竖直墙上,另一端系于物体上(∠BAC=θ=60°),在物体上另施加一个方向与水平线也成θ角的拉力F,若要使绳都能伸直,下列F中不可能的是(取g=10m/s2)( )
如图所示,物体的质量为2kg,两根轻细绳AB和AC的一端固定于竖直墙上,另一端系于物体上(∠BAC=θ=60°),在物体上另施加一个方向与水平线也成θ角的拉力F,若要使绳都能伸直,下列F中不可能的是(取g=10m/s2)( )
 如图所示,物体的质量为2kg,两根轻细绳AB和AC的一端固定于竖直墙上,另一端系于物体上(∠BAC=θ=60°),在物体上另施加一个方向与水平线也成θ角的拉力F,若要使绳都能伸直,下列F中不可能的是(取g=10m/s2)( )
如图所示,物体的质量为2kg,两根轻细绳AB和AC的一端固定于竖直墙上,另一端系于物体上(∠BAC=θ=60°),在物体上另施加一个方向与水平线也成θ角的拉力F,若要使绳都能伸直,下列F中不可能的是(取g=10m/s2)( )| A. | 4$\sqrt{3}$N | B. | 8$\sqrt{3}$N | C. | 12$\sqrt{3}$N | D. | 16$\sqrt{3}$N |
1.做“研究平抛运动”的实验时,让小球多次沿同一轨道运动,通过描点法画小球做平抛运动的轨迹,为了能准确地描绘运动轨迹,下面列出了一些操作要求,你认为不正确的是( )
| A. | 通过调节使斜槽的末端保持水平 | |
| B. | 每次释放小球的位置可以不同 | |
| C. | 每次必须由静止释放小球 | |
| D. | 小球运动时不应与木板上的白纸(或方格纸)相接触 |
2.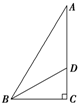 如图所示,斜面AB、DB动摩擦因数相同.可视为质点的物体分别沿AB、DB从斜面顶端由静止下滑到底端,下列说法正确的是( )
如图所示,斜面AB、DB动摩擦因数相同.可视为质点的物体分别沿AB、DB从斜面顶端由静止下滑到底端,下列说法正确的是( )
 如图所示,斜面AB、DB动摩擦因数相同.可视为质点的物体分别沿AB、DB从斜面顶端由静止下滑到底端,下列说法正确的是( )
如图所示,斜面AB、DB动摩擦因数相同.可视为质点的物体分别沿AB、DB从斜面顶端由静止下滑到底端,下列说法正确的是( )| A. | 物体沿斜面AB滑动过程中克服摩擦力做的功较多 | |
| B. | 物体沿斜面DB滑动过程中克服摩擦力做的功较多 | |
| C. | 物体沿斜面AB滑动到底端时动能较大 | |
| D. | 物体沿斜面DB滑动到底端时动能较大 |
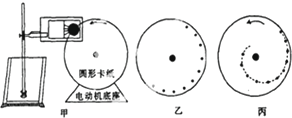
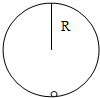 如图,光滑的竖直圆轨道半径为R,一个小球在其内侧运动.已知小球恰好通过轨道的最高点,若重力加速度为g,
如图,光滑的竖直圆轨道半径为R,一个小球在其内侧运动.已知小球恰好通过轨道的最高点,若重力加速度为g,