题目内容
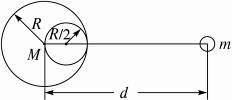
半径为R、质量为M的铅球内有一半径为R/2的球形空腔，空腔表面与铅球面内切，求这个空腔铅球以多大的力吸引质量为m的小球（体积不计）．已知小球离铅球中心的距离为d，且在铅球中心与空腔中心的连线上，如图所示．
??（4GmM/7）［2/d2-1/(2d-R)2］?
??解析一：如图所示，设想把挖去部分用与铅球同密度的材料填充，填充后铅球的质量为M0.为了抵消填充球体产生的引力，我们在右边等距处又放置一个等质量的球体，球体质量为M1，由前面运算知M1=M/7，M0=M+M1=8M/7.则
??F=F0-F1=GmM0/d2-GmM1/(d-R/2)2=8GmM/7d2-4GmM/7(2d-R)2=(4GmM/7)［2/d2-1/(2d-R)2］.
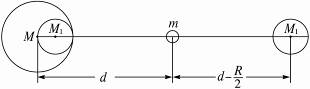
??解析二：如图所示，设想把挖去部分用与铅球同密度的材料填充，填充后铅球的质量为M0，则完整铅球对小球的吸引力可以看成是空腔铅球对小球的引力F1与填充材料对小球的引力的合力即F0=F1+F2则F1=F0-F2=GmM0/d2-GmM1/(d-R/2)2=8GmM/7d2-4GmM/7(2d-R)2=(4GmM/7)［2/d2-1/(2d-R)2］.
??F=F0-F1=GmM0/d2-GmM1/(d-R/2)2=8GmM/7d2-4GmM/7(2d-R)2=(4GmM/7)［2/d2-1/(2d-R)2］.
??解析二：如图所示，设想把挖去部分用与铅球同密度的材料填充，填充后铅球的质量为M0，则完整铅球对小球的吸引力可以看成是空腔铅球对小球的引力F1与填充材料对小球的引力的合力即F0=F1+F2则F1=F0-F2=GmM0/d2-GmM1/(d-R/2)2=8GmM/7d2-4GmM/7(2d-R)2=(4GmM/7)［2/d2-1/(2d-R)2］.
练习册系列答案
相关题目
v1。已知某星球的半径为r，它表面的重力加速度为地球重力加速度g的1/6。不计其它星球的影响。则该星球的第二宇宙速度为
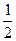，火星的质量是地球质量的
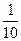，忽略火星的自转，若地球上质量为60 kg的人到火星上去，则此人在火星上的质量为___________________kg，所受重力是_______________N.在火星表面由于火星的引力产生的加速度是_______________m/s2，在地球上可举起60 kg杠铃的人到火星上用同样的力可举起质量是_______________kg的物体.已知地球表面的重力加速度g="9.8" m/s2.
?
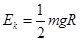
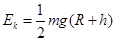
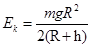
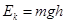
：1 D．4：1