题目内容
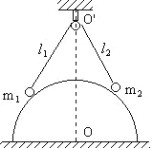
【题目】如图所示，两个小球a、b质量分别为m、2m，用细线相连并悬挂于O点，现用一轻质弾簧给小球a施加一个拉力F，使整个装置处于静止状态，且Oa与竖直方向夹角为
＝45°，已知弹簧劲度系数为k，重力加速度为g，则弹簧最短伸长量为( )
A. 
B. 
C. 
D. 
【答案】C
【解析】
以小球a、b整体为研究对象，分析受力，作出F在几个方向时整体的受力图，
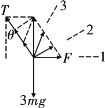
根据平衡条件得知F与T的合力与整体重力3mg总是大小相等、方向相反，由力的合成图可知，当F与绳子Oa垂直时，F有最小值，即图中2位置，F的最小值为
，
根据胡克定律
，
所以
A．与计算结果不相符,故A错误
B．与计算结果不相符,故B错误
C．与计算结果相符,故 C正确
D．与计算结果不相符,故D错误
练习册系列答案
相关题目
【题目】在“探究弹力和弹簧伸长的关系”时，某同学把两根弹簧如图1连接起来进行探究。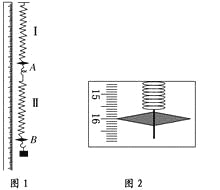
钩码数 | 1 | 2 | 3 | 4 |
LA/cm | 15．71 | 19．71 | 23．66 | 27．76 |
LB/cm | 29．96 | 35．76 | 41．51 | 47．36 |
（1）某次测量如图2所示，指针示数为________cm。
（2）在弹性限度内，将50 g的钩码逐个挂在弹簧下端，得到指针A、B的示数LA和LB如表。用表中数据计算弹簧Ⅰ的劲度系数为________N/m（重力加速度g＝10 m/s2）。由表中数据________（填“能”或“不能”）计算出弹簧Ⅱ的劲度系数。
