题目内容
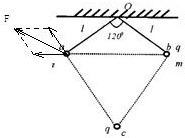
（2010?杭州二模）如图所示，将两个摆长均为l的单摆悬于O点，摆球质量均为m，带电量均为q（q＞0）．将另一个带电量也为q（q＞0）的小球从O点正下方较远处缓慢移向O点，当三个带电小球分别处在等边三角形abc的三个顶点上时，摆线的夹角恰m好为120°，则此时摆线上的拉力大小等于（ ）分析：对三个带电小球整体受力分析，则带电小球间的静电力均变为内力，不要考虑，然后根据平衡条件并运用合成法求解即可．
解答：解：因电量相同，根据库仑定律，则有：Fc=Fb=
；
由力的平行四边形定则（如图所示）可知，两库仑力的合力，则为：F=
以一个带电小球为研究对象，受重力和细绳的拉力，及另两个电荷对它的库仑力的合力F，如下图所示：
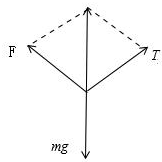
由几何关系可知，F与T的夹角也为120°，
因此根据平衡条件，得到
F=T=mg=
，故C正确，ABD错误；
故选：C．
| kq2 |
| l2 |
由力的平行四边形定则（如图所示）可知，两库仑力的合力，则为：F=
| 3 |
| kq2 |
| l2 |
以一个带电小球为研究对象，受重力和细绳的拉力，及另两个电荷对它的库仑力的合力F，如下图所示：
由几何关系可知，F与T的夹角也为120°，
因此根据平衡条件，得到
F=T=mg=
| 3 |
| kq2 |
| l2 |
故选：C．
点评：本题关键在于巧妙地选择研究对象进行受力分析，否则就会使简单问题复杂化．
练习册系列答案
阅读快车系列答案
相关题目
（2010?杭州二模）坐标原点O处有一点状的放射源，它向xoy平面内的x轴上方各个方向发射α粒子，α粒子的速度大小都是v0，在0＜y＜d的区域内分布有指向y轴正方向的匀强电场，场强大小为
（2010?杭州二模）如图所示，用三块完全相同的两面平行玻璃组成一等边三角形．由红光和蓝光组成的一细光束以平行BC面的方向从AB面射入，由AC面射出，则从AC面射出的光（ ）