题目内容
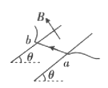
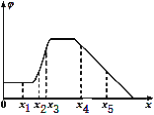
【题目】如图甲所示，在两块长为
L、间距为L、水平固定的平行金属板之间，存在方向垂直纸面向外的匀强磁场。现将下板接地，让质量为m、电荷量为q的带正电粒子流从两板左端连线的中点O以初速度v0水平向右射入板间，粒子恰好打到下板的中点。若撤去平行板间的磁场，使上板的电势随时间t的变化规律如图乙所示，则t＝0时刻，从0点射入的粒子P经时间（未知量）恰好从下板右边缘射出。设粒子打到板上均被板吸收，粒子的重力及粒子间的作用力均不计。
（1）求两板间磁场的磁感应强度大小B。
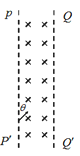
（2）若两板右侧存在一定宽度的、方向垂直纸面向里的匀强磁场，为了使t＝0时刻射入的粒子P经过右侧磁场偏转后在电场变化的第一个周期内能够回到0点，求右侧磁场的宽度d应满足的条件和电场周期T的最小值Tmin。
【答案】（1）
（2）
； 
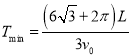
【解析】（1）设粒子在两板间做匀速圆周运动的半径为R1．由洛伦兹力提供向心力有：
根据几何关系有：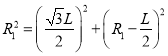 
解得： 
（2）粒子P从O点运动到下板右边缘的过程，有： 
解得： 
设合速度为v．与竖直方向的夹角为，则tan＝
，即
粒子P在两板的右侧匀强磁场中做匀速圆周运动，设做圆周运动的半径为R2，有：
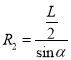
解得： 
右侧磁场沿初速度方向的宽度成满足的条件为： 
由于粒子P从O点运动到下板右边缘的过程与从上板右边缘运动到0点的过程，运动轨迹关于两板间的中心线是上下对称的，这两个运动过程经历的时间相等。有：
解得：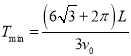 
练习册系列答案
相关题目
