题目内容
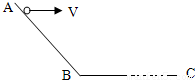 如图所示,AB为斜面,BC水平面.从A点以水平初速度v向右抛出一小球,其第一落点与A的水平距离为s1;从A点以水平初速度2v向右抛出一小球,其第一落点与A的水平距离为s2.不计空气阻力,则s1:s2可能为( )
如图所示,AB为斜面,BC水平面.从A点以水平初速度v向右抛出一小球,其第一落点与A的水平距离为s1;从A点以水平初速度2v向右抛出一小球,其第一落点与A的水平距离为s2.不计空气阻力,则s1:s2可能为( )A.1:2
B.1:3
C.1:4
D.1:5
【答案】分析:因为不知道小球的具体落地点,所以可分三种情况进行讨论:①两次小球都落在水平面BC上;②两次小球都落在斜面AB上;③第一次落在斜面AB上,第二次落在水平面BC上.再根据平抛运动的规律即可求解.
解答:解:本题可分三种情况进行讨论:
①若两次小球都落在BC水平面上,则下落的高度相同,所以运动的时间相同,水平距离之比等于水平初速度之比为1:2,故A答案正确;
②若两次小球都落在斜面AB上,设斜面倾角为θ,则有在沿斜面垂直的方向上(注意这只是一个分运动),小球作自由落体运动,设运动的时间分别为t1和t2,z则:
第一次:tanθ=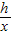 =
=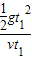 ①
①
第二次:tanθ=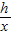 =
=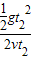 ②
②
由①②得:t1= t2
t2
所以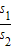 =
=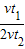 =
= 故C答案正确;
故C答案正确;
③若第一次落在斜面AB上,第二次落在水平面BC上,根据平抛运动的基本规律可知其水平位移比值在1:2到1:4之间,故B答案正确.
故选ABC.
点评:本题不知道小球的具体落地点,所以要分三种情况进行讨论,然后根据平抛运动相关知识解题,对同学们分析问题的能力要求较高,很多同学不能考虑全面,难度偏大.
解答:解:本题可分三种情况进行讨论:
①若两次小球都落在BC水平面上,则下落的高度相同,所以运动的时间相同,水平距离之比等于水平初速度之比为1:2,故A答案正确;
②若两次小球都落在斜面AB上,设斜面倾角为θ,则有在沿斜面垂直的方向上(注意这只是一个分运动),小球作自由落体运动,设运动的时间分别为t1和t2,z则:
第一次:tanθ=
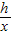 =
=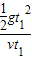 ①
①第二次:tanθ=
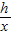 =
=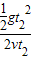 ②
②由①②得:t1=
 t2
t2所以
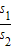 =
=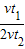 =
= 故C答案正确;
故C答案正确;③若第一次落在斜面AB上,第二次落在水平面BC上,根据平抛运动的基本规律可知其水平位移比值在1:2到1:4之间,故B答案正确.
故选ABC.
点评:本题不知道小球的具体落地点,所以要分三种情况进行讨论,然后根据平抛运动相关知识解题,对同学们分析问题的能力要求较高,很多同学不能考虑全面,难度偏大.

练习册系列答案
相关题目
 如图所示,AB为斜面,BC为水平面,从A点以水平速度v0抛出一小球,此时落点到A的水平距离为x1;从A点以水平速度3vo抛出小球,这次落点到A点的水平距离为x2,不计空气阻力,则x1:x2可能等于( )
如图所示,AB为斜面,BC为水平面,从A点以水平速度v0抛出一小球,此时落点到A的水平距离为x1;从A点以水平速度3vo抛出小球,这次落点到A点的水平距离为x2,不计空气阻力,则x1:x2可能等于( )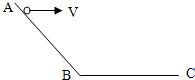 如图所示,AB为斜面,BC为水平面,从A点以水平初速度v向右抛出一小球,落点与A点的水平距离为x1.现从A点以水平初速度3v向右抛出另一小球,其落点与A点的水平距离为x2.若不计空气阻力,不考虑小球反弹,则x1:x2可能为( )
如图所示,AB为斜面,BC为水平面,从A点以水平初速度v向右抛出一小球,落点与A点的水平距离为x1.现从A点以水平初速度3v向右抛出另一小球,其落点与A点的水平距离为x2.若不计空气阻力,不考虑小球反弹,则x1:x2可能为( )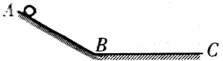 如图所示,AB为斜面,BC为水平面,从A点以水平速度v0抛出一小球,不计空气阻力,其第一次小球的落点与A点的水平距离为1m;从A点以初速度2v0水平抛出一个小球,其第一次落点与A点的水平距离为x,则下列结果有可能的是( )
如图所示,AB为斜面,BC为水平面,从A点以水平速度v0抛出一小球,不计空气阻力,其第一次小球的落点与A点的水平距离为1m;从A点以初速度2v0水平抛出一个小球,其第一次落点与A点的水平距离为x,则下列结果有可能的是( )