题目内容
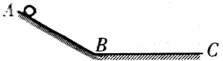 如图所示,AB为斜面,BC为水平面,从A点以水平速度v0抛出一小球,不计空气阻力,其第一次小球的落点与A点的水平距离为1m;从A点以初速度2v0水平抛出一个小球,其第一次落点与A点的水平距离为x,则下列结果有可能的是( )
如图所示,AB为斜面,BC为水平面,从A点以水平速度v0抛出一小球,不计空气阻力,其第一次小球的落点与A点的水平距离为1m;从A点以初速度2v0水平抛出一个小球,其第一次落点与A点的水平距离为x,则下列结果有可能的是( )分析:将小球水平抛出后,小球做抛体运动,可分为:(1)两次均落在斜面上;(2)两次均落在水平面上;(3)第一次落在斜面上,第二次落在水平面上.这3种情况分别列式求解.
解答:解:(1)假设两球均落到斜面上,设斜面倾角为θ;
则有在沿斜面垂直的方向上(注意这只是一个分运动),小球作类竖直上抛运动:初速度为:vsinθ,加速度为:gcosθ
由竖直上抛运动运动时间:t=
得:
则:运动时间:t1=
; t2=
,所以t2=2t1.
所以:第一次的水平距离与第二次水平距离之比为:s1:s2=(v:2v)×(t1:t2)=1:4,所以第二次的距离可能是4m.故C正确.
(2)假设两球均落到水平面上,由于下落高度相同,故下落时间相同.水平位移的比值等于初速度的比值,为1:2,所以第二次的距离可能是2m.故A正确.
(3)一个落在斜面上,另一个落在水平面上:比值介于上述两种情况之间.即:第二次的距离为2m到4m之间的数值.故B正确.
综上所述:第二次的距离的取值范围是:[2m,4m],故D错误.
故选:ABC
则有在沿斜面垂直的方向上(注意这只是一个分运动),小球作类竖直上抛运动:初速度为:vsinθ,加速度为:gcosθ
由竖直上抛运动运动时间:t=
| 2v0 |
| g |
则:运动时间:t1=
| 2vsinθ |
| gcosθ |
| 2×2vsinθ |
| gcosθ |
所以:第一次的水平距离与第二次水平距离之比为:s1:s2=(v:2v)×(t1:t2)=1:4,所以第二次的距离可能是4m.故C正确.
(2)假设两球均落到水平面上,由于下落高度相同,故下落时间相同.水平位移的比值等于初速度的比值,为1:2,所以第二次的距离可能是2m.故A正确.
(3)一个落在斜面上,另一个落在水平面上:比值介于上述两种情况之间.即:第二次的距离为2m到4m之间的数值.故B正确.
综上所述:第二次的距离的取值范围是:[2m,4m],故D错误.
故选:ABC
点评:抛体运动的处理要按照加速度不变这个本质的主题去处理,找准运动的情形,分别列式即可.

练习册系列答案
相关题目
 如图所示,AB为斜面,BC为水平面,从A点以水平速度v0抛出一小球,此时落点到A的水平距离为x1;从A点以水平速度3vo抛出小球,这次落点到A点的水平距离为x2,不计空气阻力,则x1:x2可能等于( )
如图所示,AB为斜面,BC为水平面,从A点以水平速度v0抛出一小球,此时落点到A的水平距离为x1;从A点以水平速度3vo抛出小球,这次落点到A点的水平距离为x2,不计空气阻力,则x1:x2可能等于( )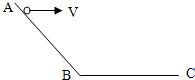 如图所示,AB为斜面,BC为水平面,从A点以水平初速度v向右抛出一小球,落点与A点的水平距离为x1.现从A点以水平初速度3v向右抛出另一小球,其落点与A点的水平距离为x2.若不计空气阻力,不考虑小球反弹,则x1:x2可能为( )
如图所示,AB为斜面,BC为水平面,从A点以水平初速度v向右抛出一小球,落点与A点的水平距离为x1.现从A点以水平初速度3v向右抛出另一小球,其落点与A点的水平距离为x2.若不计空气阻力,不考虑小球反弹,则x1:x2可能为( )