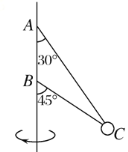
[题目]如图所示.两轻绳系一个质量为m的小球.两绳的另一端分别固定于轴的A.B两处.上面的绳长l＝2 m.两绳都拉直时与轴夹角分别为30°和45°.则小球随轴转动的角速度ω满足什么条件时.两绳始终被拉直．(g取10 m/s2.结果保留两位有效数字) 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图所示，两轻绳系一个质量为m的小球，两绳的另一端分别固定于轴的A、B两处，上面的绳长l＝2 m，两绳都拉直时与轴夹角分别为30°和45°，则小球随轴转动的角速度ω满足什么条件时，两绳始终被拉直．（g取10 m/s2，结果保留两位有效数字）

【答案】2．4 rad/s≤ω≤3．2 rad/s

【解析】

试题分析：ω由0逐渐增大时，将出现两个临界值．当绳BC恰好被拉直但无拉力时，小球受重力mg、绳AC的拉力F1，如图所示．

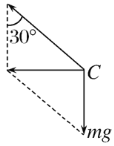
设此时的角速度为ω1，由牛顿第二定律得mgtan30°＝mωlsin30°

代入数据解得ω1＝2．4 rad/s

当绳AC恰好被拉直但无拉力时，小球受重力mg、绳BC的拉力F2，设此时的角速度为ω2．由牛顿第二定律得mgtan45° ＝ mωlsin30°

代入数据解得ω2＝3．2 rad/s

可见，要使两绳始终被拉直，ω必须满足条件2．4 rad/s≤ω≤3．2 rad/s．

练习册系列答案

（1）求出磁感应强度B的大小和ab棒加速度大小；

（2）已知在2 s内外力F做功40 J，求此过程中两金属棒产生的总焦耳热；

（3）求出cd棒达到最大速度所需的时间。

【题目】我国发射神舟号飞船时，先将飞船发送到一个椭圆轨道上，其近地点M距地面200km，远地点N距地面340km．进入该轨道正常运行时，通过M、N点时的速率分别是v1、v2．当某次飞船通过N点时，地面指挥部发出指令，点燃飞船上的发动机，使飞船在短时间内加速后进入离地面340km的圆形轨道，开始绕地球做匀速圆周运动．这时飞船的速率为v3．比较飞船在M、N、P三点正常运行时（不包括点火加速阶段）的速率大小和加速度大小，下列结论正确的是（）

A. v1＞v3＞v2，a1＞a3＞a2

B. v1＞v3＞v2，a1＞a2=a3

C. v1＞v2=v3，a1＞a2＞a3

D. v1＞v2＞v3，a1＞a2=a3

【题目】一探险队员在探险时遇到一山沟，山沟的一侧竖直，另一侧的坡面呈抛物线形状。此队员从山沟的竖直一侧，以速度v0沿水平方向跳向另一侧坡面。如图所示，以沟底的O点为原点建立坐标系Oxy。已知，山沟竖直一侧的高度为h，坡面的抛物线方程为y=，探险队员的质量为m。人视为质点，忽略空气阻力，重力加速度为g。