题目内容
10. 如图所示,一光滑的半径为R的半圆形轨道放在水平面上,一个质量为m的小球以某一速度冲上轨道,当小球将要从轨道口飞出时,轨道的压力恰好为零,则( )
如图所示,一光滑的半径为R的半圆形轨道放在水平面上,一个质量为m的小球以某一速度冲上轨道,当小球将要从轨道口飞出时,轨道的压力恰好为零,则( )| A. | 小球落地点C距A处2R | B. | 小球落地点C距A处$\sqrt{2R}$ | ||
| C. | 小球冲上轨道前的速度是$\sqrt{3gR}$ | D. | 小球冲上轨道前的速度是$\sqrt{5gR}$ |
分析 小球在B点只受重力,重力提供向心力,根据牛顿第二定律列式即可求解C点速度;从轨道口B处水平飞出后,小球做平抛运动,由平抛运动的规律可以求得C到A的距离.由机械能守恒求小球冲上轨道前的速度.
解答 解:设小球脱离轨道到落地时间为t,脱离时速度为v,由平抛运动可得:
h=$\frac{1}{2}g{t^2}$=2R,可推得:t=$\sqrt{\frac{4R}{g}}$,
又因为在B点,轨道对小球的压力刚好为0,则有:mg=m$\frac{{v}^{2}}{R}$,
得:v=$\sqrt{gR}$
所以x=vt=2R,即小球落地点C距A处2R.
根据机械能守恒定律得:-2mgR=$\frac{1}{2}m{v^2}-\frac{1}{2}m{v_0}^2$
可得小球冲上轨道前的速度是:v0=$\sqrt{5gR}$
故选:AD.
点评 本题是牛顿第二定律、向心力公式、平抛运动规律的综合运用问题,关键理清小球的运动情况,然后分阶段列式求解.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
20. 在匀强磁场中有一个线圈,如图所示,当线圈分别以P1和P2为轴,按逆时针方向以相同角速度转动时,线圈中产生的感应电流的最大值分别为Im1和Im2,则Im1和Im2的大小关系为( )
在匀强磁场中有一个线圈,如图所示,当线圈分别以P1和P2为轴,按逆时针方向以相同角速度转动时,线圈中产生的感应电流的最大值分别为Im1和Im2,则Im1和Im2的大小关系为( )
 在匀强磁场中有一个线圈,如图所示,当线圈分别以P1和P2为轴,按逆时针方向以相同角速度转动时,线圈中产生的感应电流的最大值分别为Im1和Im2,则Im1和Im2的大小关系为( )
在匀强磁场中有一个线圈,如图所示,当线圈分别以P1和P2为轴,按逆时针方向以相同角速度转动时,线圈中产生的感应电流的最大值分别为Im1和Im2,则Im1和Im2的大小关系为( )| A. | Im1大于Im2 | B. | Im1小于Im2 | ||
| C. | Im1等于Im2 | D. | 以上情况均有可能 |
1.从空中以10m/s的初速度沿着水平方向抛出一个重为10N的物体,已知t=3s时物体未落地,不计空气阻力,取g=10m/s2,则以下说法正确的是( )
| A. | 抛出后3s末,小球的速度为40m/s | |
| B. | 抛出后(末落地)任意时间内,速度改变量的方向竖直向下 | |
| C. | 在抛出3s末,重力的功率为300W | |
| D. | 在抛出3s内,重力的平均功率为450W |
18. 在倾角为θ的斜面上固定两根足够长的光滑平行金属导轨PQ、MN,相距为L,导轨处于磁感应强度为B的匀强磁场中,磁场方向垂直导轨平面向下.有两根质量均为m的金属棒a、b,先将a 棒垂直导轨放置,用跨过光滑定滑轮的细线与物块c 连接,连接a棒的细线平行于导轨,由静止释放c,此后某时刻,将b也垂直导轨放置,a、c此刻起做匀速运动,b棒刚好能静止在导轨上.a棒在运动过程中始终与导轨垂直,两棒与导轨接触良好,导轨电阻不计.则( )
在倾角为θ的斜面上固定两根足够长的光滑平行金属导轨PQ、MN,相距为L,导轨处于磁感应强度为B的匀强磁场中,磁场方向垂直导轨平面向下.有两根质量均为m的金属棒a、b,先将a 棒垂直导轨放置,用跨过光滑定滑轮的细线与物块c 连接,连接a棒的细线平行于导轨,由静止释放c,此后某时刻,将b也垂直导轨放置,a、c此刻起做匀速运动,b棒刚好能静止在导轨上.a棒在运动过程中始终与导轨垂直,两棒与导轨接触良好,导轨电阻不计.则( )
 在倾角为θ的斜面上固定两根足够长的光滑平行金属导轨PQ、MN,相距为L,导轨处于磁感应强度为B的匀强磁场中,磁场方向垂直导轨平面向下.有两根质量均为m的金属棒a、b,先将a 棒垂直导轨放置,用跨过光滑定滑轮的细线与物块c 连接,连接a棒的细线平行于导轨,由静止释放c,此后某时刻,将b也垂直导轨放置,a、c此刻起做匀速运动,b棒刚好能静止在导轨上.a棒在运动过程中始终与导轨垂直,两棒与导轨接触良好,导轨电阻不计.则( )
在倾角为θ的斜面上固定两根足够长的光滑平行金属导轨PQ、MN,相距为L,导轨处于磁感应强度为B的匀强磁场中,磁场方向垂直导轨平面向下.有两根质量均为m的金属棒a、b,先将a 棒垂直导轨放置,用跨过光滑定滑轮的细线与物块c 连接,连接a棒的细线平行于导轨,由静止释放c,此后某时刻,将b也垂直导轨放置,a、c此刻起做匀速运动,b棒刚好能静止在导轨上.a棒在运动过程中始终与导轨垂直,两棒与导轨接触良好,导轨电阻不计.则( )| A. | 物块c的质量是2msinθ | |
| B. | b棒放上导轨前,物块c减少的重力势能等于a、c增加的动能 | |
| C. | b棒放上导轨后,物块c减少的重力势能等于回路消耗的电能与a增加的重力势能之和 | |
| D. | b棒放上导轨后,a棒中电流大小是$\frac{mgsinθ}{BL}$ |
16. 如右图所示的电路中,线圈L用铜导线绕制而成,其自感系数很大,电阻忽略不计,开关S原来闭合,当开关S断开瞬间,则( )
如右图所示的电路中,线圈L用铜导线绕制而成,其自感系数很大,电阻忽略不计,开关S原来闭合,当开关S断开瞬间,则( )
 如右图所示的电路中,线圈L用铜导线绕制而成,其自感系数很大,电阻忽略不计,开关S原来闭合,当开关S断开瞬间,则( )
如右图所示的电路中,线圈L用铜导线绕制而成,其自感系数很大,电阻忽略不计,开关S原来闭合,当开关S断开瞬间,则( )| A. | 电容器A板带负电 | B. | L中的电流方向不变 | ||
| C. | 灯泡D要过一会儿才熄灭 | D. | 刚断开瞬间,电容器中的电场为零 |
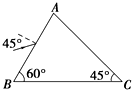 一束光波以45°的入射角,从AB面射入如图所示的透明三棱镜中,棱镜折射率n=$\sqrt{2}$.试求
一束光波以45°的入射角,从AB面射入如图所示的透明三棱镜中,棱镜折射率n=$\sqrt{2}$.试求
 F B.
F B. F C.
F C. F D.
F D. F
F 如图所示,质量均为m的物体A、B通过一劲度系数为k的轻弹簧相连,开始时B放在地面上,A、B都处于静止状态.现用手通过细绳缓慢地将A向上提升距离L1时,B刚要离开地面,此过程中手做功为W1;若将A加速向上拉起,A上升的距离为L2时,B刚要离开地面,此过程中手做功为W2.设弹簧一直在弹性限度范围内,则( )
如图所示,质量均为m的物体A、B通过一劲度系数为k的轻弹簧相连,开始时B放在地面上,A、B都处于静止状态.现用手通过细绳缓慢地将A向上提升距离L1时,B刚要离开地面,此过程中手做功为W1;若将A加速向上拉起,A上升的距离为L2时,B刚要离开地面,此过程中手做功为W2.设弹簧一直在弹性限度范围内,则( )