题目内容
1.从空中以10m/s的初速度沿着水平方向抛出一个重为10N的物体,已知t=3s时物体未落地,不计空气阻力,取g=10m/s2,则以下说法正确的是( )| A. | 抛出后3s末,小球的速度为40m/s | |
| B. | 抛出后(末落地)任意时间内,速度改变量的方向竖直向下 | |
| C. | 在抛出3s末,重力的功率为300W | |
| D. | 在抛出3s内,重力的平均功率为450W |
分析 根据高度求出平抛运动的时间,结合速度时间公式求出3s时竖直分速度,根据平行四边形定则求出小球的速度.根据瞬时功率的公式求出瞬时功率的大小,结合平均功率的公式求出重力做功的平均功率.
解答 解:A、3s时竖直分速度vy=gt=10×3m/s=30m/s,根据平行四边形定则知,小球的速度v=$\sqrt{{{v}_{0}}^{2}+{{v}_{y}}^{2}}$=$\sqrt{100+900}$m/s=10$\sqrt{10}$m/s,故A错误.
B、因为平抛运动的加速度竖直向下,则任意一段时间内的速度变化量的方向竖直向下,故B正确.
C、3s末重力的瞬时功率P=mgvy=10×30W=300W,故C正确.
D、3s内重力做功的平均功率P=$\frac{mgh}{t}=\frac{mg•\frac{1}{2}g{t}^{2}}{t}=\frac{1}{2}m{g}^{2}t$=$\frac{1}{2}×1×100×3W$=150W,故D错误.
故选:BC.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,知道平均功率和瞬时功率的区别,掌握这两种功率的求法.

练习册系列答案
相关题目
12.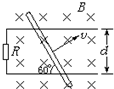 如图所示,两根相距d平行放置的导电轨道,轨道间接有电阻R,处于磁感应强为B,垂直轨道平面内的匀强磁场中,一根金属杆与轨道成60°角放置在轨道上,现让金属杆以垂直于杆的速度v沿轨道匀速滑行,若导电轨道和金属杆的电阻不计,则通过电阻R的电流为( )
如图所示,两根相距d平行放置的导电轨道,轨道间接有电阻R,处于磁感应强为B,垂直轨道平面内的匀强磁场中,一根金属杆与轨道成60°角放置在轨道上,现让金属杆以垂直于杆的速度v沿轨道匀速滑行,若导电轨道和金属杆的电阻不计,则通过电阻R的电流为( )
 如图所示,两根相距d平行放置的导电轨道,轨道间接有电阻R,处于磁感应强为B,垂直轨道平面内的匀强磁场中,一根金属杆与轨道成60°角放置在轨道上,现让金属杆以垂直于杆的速度v沿轨道匀速滑行,若导电轨道和金属杆的电阻不计,则通过电阻R的电流为( )
如图所示,两根相距d平行放置的导电轨道,轨道间接有电阻R,处于磁感应强为B,垂直轨道平面内的匀强磁场中,一根金属杆与轨道成60°角放置在轨道上,现让金属杆以垂直于杆的速度v沿轨道匀速滑行,若导电轨道和金属杆的电阻不计,则通过电阻R的电流为( )| A. | $\frac{Bdv}{{Rsin{{60}°}}}$ | B. | $\frac{Bdv}{R}$ | C. | $\frac{{Bdvsin{{60}°}}}{R}$ | D. | $\frac{{Bdvcos{{60}°}}}{R}$ |
16. 用电高峰期,电灯往往会变暗,其原理可简化为如下物理问题,如图所示,理想变压器副线圈上,通过输电线连接两只相同的灯泡L1和L2,输电线的等效电阻为R,原线圈输入有效值恒定的交流电压,当开关S闭合时,以下说法中正确的是( )
用电高峰期,电灯往往会变暗,其原理可简化为如下物理问题,如图所示,理想变压器副线圈上,通过输电线连接两只相同的灯泡L1和L2,输电线的等效电阻为R,原线圈输入有效值恒定的交流电压,当开关S闭合时,以下说法中正确的是( )
 用电高峰期,电灯往往会变暗,其原理可简化为如下物理问题,如图所示,理想变压器副线圈上,通过输电线连接两只相同的灯泡L1和L2,输电线的等效电阻为R,原线圈输入有效值恒定的交流电压,当开关S闭合时,以下说法中正确的是( )
用电高峰期,电灯往往会变暗,其原理可简化为如下物理问题,如图所示,理想变压器副线圈上,通过输电线连接两只相同的灯泡L1和L2,输电线的等效电阻为R,原线圈输入有效值恒定的交流电压,当开关S闭合时,以下说法中正确的是( )| A. | 原线圈中的电流增大 | B. | R两端的电压增大 | ||
| C. | 原线圈输入功率不变 | D. | 副线圈输出电压减小 |
6. 将一小球以水平速度v0=10m/s从O点向右抛出,经1.73s小球恰好垂直落到斜面上的A点,不计空气阻力,g=10m/s2,B点是小球做自由落体运动在斜面上的落点,如图所示,以下判断正确的是( )
将一小球以水平速度v0=10m/s从O点向右抛出,经1.73s小球恰好垂直落到斜面上的A点,不计空气阻力,g=10m/s2,B点是小球做自由落体运动在斜面上的落点,如图所示,以下判断正确的是( )
 将一小球以水平速度v0=10m/s从O点向右抛出,经1.73s小球恰好垂直落到斜面上的A点,不计空气阻力,g=10m/s2,B点是小球做自由落体运动在斜面上的落点,如图所示,以下判断正确的是( )
将一小球以水平速度v0=10m/s从O点向右抛出,经1.73s小球恰好垂直落到斜面上的A点,不计空气阻力,g=10m/s2,B点是小球做自由落体运动在斜面上的落点,如图所示,以下判断正确的是( )| A. | 斜面的倾角约是30° | |
| B. | 小球的抛出点距斜面的竖直高度约是15 m | |
| C. | 若将小球以水平速度v0′=5 m/s向右抛出,它一定落在AB的中点P的上方 | |
| D. | 若将小球以水平速度v0′=5 m/s向右抛出,它一定落在AB的中点P处 |
10. 如图所示,一光滑的半径为R的半圆形轨道放在水平面上,一个质量为m的小球以某一速度冲上轨道,当小球将要从轨道口飞出时,轨道的压力恰好为零,则( )
如图所示,一光滑的半径为R的半圆形轨道放在水平面上,一个质量为m的小球以某一速度冲上轨道,当小球将要从轨道口飞出时,轨道的压力恰好为零,则( )
 如图所示,一光滑的半径为R的半圆形轨道放在水平面上,一个质量为m的小球以某一速度冲上轨道,当小球将要从轨道口飞出时,轨道的压力恰好为零,则( )
如图所示,一光滑的半径为R的半圆形轨道放在水平面上,一个质量为m的小球以某一速度冲上轨道,当小球将要从轨道口飞出时,轨道的压力恰好为零,则( )| A. | 小球落地点C距A处2R | B. | 小球落地点C距A处$\sqrt{2R}$ | ||
| C. | 小球冲上轨道前的速度是$\sqrt{3gR}$ | D. | 小球冲上轨道前的速度是$\sqrt{5gR}$ |

 如图所示,两物块A、B分别系在一条跨过定滑轮的软绳两端,利用光电门验证A、B所构成的系统机械能守恒.
如图所示,两物块A、B分别系在一条跨过定滑轮的软绳两端,利用光电门验证A、B所构成的系统机械能守恒.
 如图所示为“研究平抛物体的运动”的实验.
如图所示为“研究平抛物体的运动”的实验.