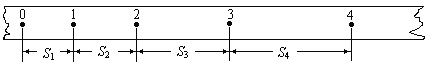��Ŀ����
����Ŀ����ͼ��ʾ�������뾶Ϊr��![]() Բ��������ΪL���䶥��a��b��Բ�Ĵ��ȸߣ�����⻬�ҵ��費�ƣ������϶�����һ��ֵΪR�ĵ��裬����װ�ô��ڷ���ų��У�Բ��������ڴ��ĴŸ�Ӧǿ�ȴ�С��ΪB����һ�������Դ���L������Ϊm������ΪR0�Ľ������ӹ������ab���ɾ�ֹ�ͷţ���֪��������������ͼ��ʾ��cdλ�ã�����������Բ�����ߺ�ˮƽ��н�Ϊ����ʱ�����������ٶȴﵽ�����������������efʱ���Թ����ѹ��Ϊ1.5mg����
Բ��������ΪL���䶥��a��b��Բ�Ĵ��ȸߣ�����⻬�ҵ��費�ƣ������϶�����һ��ֵΪR�ĵ��裬����װ�ô��ڷ���ų��У�Բ��������ڴ��ĴŸ�Ӧǿ�ȴ�С��ΪB����һ�������Դ���L������Ϊm������ΪR0�Ľ������ӹ������ab���ɾ�ֹ�ͷţ���֪��������������ͼ��ʾ��cdλ�ã�����������Բ�����ߺ�ˮƽ��н�Ϊ����ʱ�����������ٶȴﵽ�����������������efʱ���Թ����ѹ��Ϊ1.5mg����

(1)�����������ٶ����ʱ����������R�ĵ�����С�ͷ���(��a��R��b��b��R��a)��
(2)��������������˵�������������������R�ĵ�����
(3)��������������˵����������е���R�ϲ�����������
���𰸡�(1) ![]() ,����Ϊa��R��b (2)
,����Ϊa��R��b (2) ![]() (3)
(3) ![]()
�������������������1���������ٶ����ʱ���ڹ�����߷������ܺ���Ϊ0���ɴ�������ʽ�����������R�ĵ�����С�������ֶ����жϵ�������
��2���������»������У���·�Ĵ�ͨ�����ӣ��������ͨ���������������ɷ����ڵ�Ÿ�Ӧ���ɺ�ŷķ�����������
��3������ţ�ٵڶ��������������������͵�ʱ���ٶȣ��ٸ��������غ㶨�������R�ϲ�����������
�⣺��1���������ٶ����ʱ���ڹ�����߷������ܺ���Ϊ0�����У�
mgcos��=BIL
��ã�I=![]() ������R�ĵ�������Ϊa��R��b��
������R�ĵ�������Ϊa��R��b��
��2����������������˵����������У�������·�Ĵ�ͨ���仯��Ϊ��
����=BS=BL![]() =
=![]()
ƽ���綯��Ϊ��![]() =
=![]() ��ƽ������Ϊ��
��ƽ������Ϊ��![]() =
=![]()
����������R�ĵ�����q=![]() t=
t=![]() =
=![]()
��3���ڹ����͵�ʱ����ţ�ٵڶ����ɵã�N��mg=m![]()
������N=1.5mg
������ת�����غ�ã�Q=mgr��![]() =
=![]() mgr
mgr
����R�Ϸ�����Ϊ��QR=![]() Q=
Q=![]()
�𣺣�1�������������ٶ����ʱ����������R�ĵ�����СΪ![]() ������R�ĵ�������Ϊa��R��b��
������R�ĵ�������Ϊa��R��b��
��2����������������˵�������������������R�ĵ���Ϊ![]() ��
��
��3����������������˵����������е���R�ϲ���������Ϊ![]() ��
��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�