题目内容
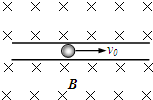
在一绝缘、粗糙且足够长的水平管道中有一带电量为q、质量为m的带电球体,管道半径略大于球体半径.整个管道处于磁感应强度为B的水平匀强磁场中,磁感应强度方向与管道垂直.现给带电球体一个水平速度v0,则在整个运动过程中,带电球体克服摩擦力所做的功可能为( )
| A.0 | B.
| ||||||||
C.
| D.
|

(1)当qv0B=mg时,圆环不受支持力和摩擦力,摩擦力做功为零,故A正确.
(2)当qv0B<mg时,圆环做减速运动到静止,只有摩擦力做功.根据动能定理得
-W=0-
mv02得W=
mv02故C正确.
(3)当qv0B>mg时,圆环先做减速运动,当qvB=mg,即当qvB=mg,v=
时,不受摩擦力,做匀速直线运动.
根据动能定理得:-W=
mv2-
m
,代入解得:W=
m[
+(
)2]故D正确.
故选ACD.
(2)当qv0B<mg时,圆环做减速运动到静止,只有摩擦力做功.根据动能定理得
-W=0-
| 1 |
| 2 |
| 1 |
| 2 |
(3)当qv0B>mg时,圆环先做减速运动,当qvB=mg,即当qvB=mg,v=
| mg |
| qB |
根据动能定理得:-W=
| 1 |
| 2 |
| 1 |
| 2 |
| v | 20 |
| 1 |
| 2 |
| v | 20 |
| mg |
| qB |
故选ACD.

练习册系列答案
相关题目






 v,仍从A点沿原方向射入磁场,不计重力,则粒子在磁场中的运动时间变为
v,仍从A点沿原方向射入磁场,不计重力,则粒子在磁场中的运动时间变为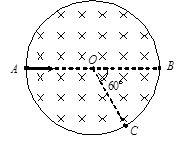
 Δt
Δt Δt
Δt Δt
Δt