Question

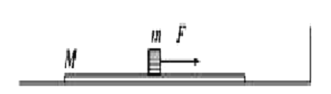
【题目】如图，在光滑水平轨道的右方有一弹性挡板，一质量为M＝0.5kg的木板正中间放有一质量为m＝2kg的小铁块(可视为质点)静止在轨道上，木板右端距离挡板x0＝0.5m，小铁块与木板间动摩擦因数μ＝0.2.现对小铁块施加一水平向右的外力F，木板第一次与挡板碰前瞬间撤去外力．若木板与挡板碰撞时间极短，反弹后速度大小不变，最大静摩擦力等于滑动摩擦力，重力加速度g＝10m/s2.

(1)要使小铁块与木板发生相对滑动 求水平向右的外力F的最小值；

(2)若水平向右的外力F＝10N，求木板第一次与挡板碰撞前经历的时间；

(3)若水平向右的外力F＝10N，木板第一次与挡板碰前瞬间撤去外力，铁块和木板最终停下来时，铁块刚好没滑出木板，求木板的长度。

Answer 1

【答案】(1)20N (2) t＝0.5s (3) 2.5m

【解析】

(1)设木板靠最大静摩擦力即滑动摩擦力产生的加速度为am，则，

am＝＝8m/s2

对铁块和木板组成的整体得：

得：

=20N

(2)因F＜，所以木板在静摩擦力作用下与铁块一起以加速度a运动．

设共同加速度为a；

a＝＝4m/s2

设向右运动第一次与挡板碰撞前经历的时间为t，则

x0＝at2

解得

t＝0.5 s

(3)设木板与挡板碰前，木板与物块的共同速度为v1，则v1＝at，解得

v1＝2 m/s

木板第一次与挡板碰撞前瞬间撤去外力，物块以速度v1向右做减速运动，加速度大小为a1，木板与挡板碰撞后以速度v1向左做减速运动，木板与木块相对滑动，则木板加速度大小为am，设板速度减为零经过的时间为t1，向左运动的最远距离为x1，则

μmg＝ma1 ；v1＝amt1 ；x1＝

解得

a1＝2 m/s2，t1＝0.25 s，x1＝0.25 m

当板速度向左为零时，设铁块速度为v1′，则

v1′＝v1－a1t1

设再经过时间t2铁块与木板达到共同速度v2，木板向右位移为x1′，则

v2＝v1′－a1t2，v2＝amt2，x1′＝amt

解得

v1′＝1.5 m/s，t2＝0.15s，v2＝1.2 m/s，x1′＝0.09 m

因为x1′＜x1，所以木板与铁块达到共速后，将以速度v2运动，再次与挡板碰撞．以后多次重复这些过程最终木板停在挡板处．以木板和铁块系统为研究对象，根据能量守恒

μmgS＝ (m＋M)

设木板长为L，解得

L＝2S=2.5 m