题目内容
【题目】如图所示,光滑斜轨和光滑圆轨相连,固定在同一竖直面内,圆轨的半径为R,一个小球(可视为质点),从离水平面高h处由静止自由下滑,由斜轨进入圆轨.求: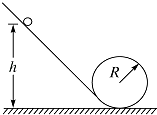
(1)为了使小球在圆轨内运动的过程中始终不脱离圆轨,h应至少多高?
(2)若小球到达圆轨最高点时圆轨对小球的压力大小恰好等于它自身重力大小,那么小球开始下滑时的h是多大?
【答案】
(1)解:小球刚好不脱离圆轨,在最高点由牛顿第二定律得: ![]() ①
①
小球由斜轨至圆轨最高点过程,由动能定理得:mg(h﹣2R)= ![]() ②
②
联立①②解得: ![]()
故 ![]() 时小球在圆轨内运动的过程中始终不脱离圆轨,高度至少为
时小球在圆轨内运动的过程中始终不脱离圆轨,高度至少为 ![]() .
.
答:h应至少为2.5R;
(2)解:在最高点对小球由牛顿第二定律得:FN+mg= ![]() ③
③
又有:FN=mg④
小球由斜轨至圆轨最高点过程,由动能定理得:mg(h﹣2R)= ![]() ⑤
⑤
联立③④⑤解得:h=3R;
答:球开始下滑时的h是3R.
【解析】(1)由竖直平面内的圆周运动的临界条件可求得最高点的速度;再由动能定理可求得h的高度;(2)最高点处对小球受力分析,由向心力公式可求得小球的速度;再由动能定理即可求得高度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目











