题目内容
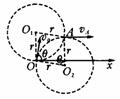
真空中有一半径为r的圆柱形匀强磁场区域,方向垂直纸面向里,Ox为过边界上O点的切线,如图所示,从O点在纸面内向各个方向发射速率均为v0的电子,设电子间相互作用忽略,且电子在磁场中偏转半径也为r,已知电子的电量为e,质量为m.(1)速度方向分别与Ox方向夹角成600和900的电子,在磁场中的运动时间分别为多少?
(2)所有从磁场边界出射的电子,速度方向有何特征?
(3)令在某一平面内有M、N两点,从M点向平面内各个方向发射速率均为v0的电子,请设计一种匀强磁场分布,其磁感应强度大小为B,使得由M点发出的电子都能够汇聚到N点.

解:(1)如图所示,入射时电子速度与x轴夹角为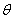 ,无论入射的速度方向与x轴的夹角为何值,入射点均为O,射出点均为A,磁场圆心O1和轨道圆心O2一定组成边长为r的菱形.因O1O⊥Ox , OO2垂直于入射速度,故∠OO2 A=
,无论入射的速度方向与x轴的夹角为何值,入射点均为O,射出点均为A,磁场圆心O1和轨道圆心O2一定组成边长为r的菱形.因O1O⊥Ox , OO2垂直于入射速度,故∠OO2 A=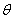 .即电子在磁场中所转过的角度一定等于入射时电子速度与Ox轴的夹角.当
.即电子在磁场中所转过的角度一定等于入射时电子速度与Ox轴的夹角.当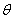 = 600时,
= 600时,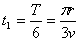 ;当
;当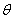 = 900时,
= 900时,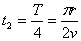 。
。 (2)因∠OO2 A=
(2)因∠OO2 A=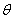 ,故O2A⊥Ox.而O2A与电子射出的速度方向垂直,可知电子射出方向一定与Ox轴方向平行,即所有的电子射出圆形磁场时,速度方向均与Ox轴相同.(3)上述的粒子路径是可逆的,(2)中从圆形磁场射出的这些速度相同的电子再进入一相同的匀强磁场后,一定会聚焦于同一点,磁场的分布如图所示,对于从M点向MN连线上方运动的电子,两磁场分别与MN相切,M、N为切点,且平行于两磁场边界圆心的连线O1O2.设MN间的距离为l,所加的磁场的边界所对应圆的半径为r,故应有2r≤l,即
,故O2A⊥Ox.而O2A与电子射出的速度方向垂直,可知电子射出方向一定与Ox轴方向平行,即所有的电子射出圆形磁场时,速度方向均与Ox轴相同.(3)上述的粒子路径是可逆的,(2)中从圆形磁场射出的这些速度相同的电子再进入一相同的匀强磁场后,一定会聚焦于同一点,磁场的分布如图所示,对于从M点向MN连线上方运动的电子,两磁场分别与MN相切,M、N为切点,且平行于两磁场边界圆心的连线O1O2.设MN间的距离为l,所加的磁场的边界所对应圆的半径为r,故应有2r≤l,即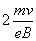 ≤l,所以所加磁场磁感应强度应满足B≥
≤l,所以所加磁场磁感应强度应满足B≥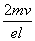 .同理,对于从M点向MN连线下方运动的电子,只要使半径相同的两圆形磁场与上方的两圆形磁场位置MN对称且磁场方向与之相反即可.
.同理,对于从M点向MN连线下方运动的电子,只要使半径相同的两圆形磁场与上方的两圆形磁场位置MN对称且磁场方向与之相反即可.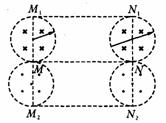 说明:只要在矩形区域M1N1N2 M2内除图中4个半圆形磁场外无其他磁场(其中M1, M2点也无磁场),矩形M1N1M2N2区域外的磁场均可向其余区域扩展.
说明:只要在矩形区域M1N1N2 M2内除图中4个半圆形磁场外无其他磁场(其中M1, M2点也无磁场),矩形M1N1M2N2区域外的磁场均可向其余区域扩展.
 (2)因∠OO2 A=
(2)因∠OO2 A= 说明:只要在矩形区域M1N1N2 M2内除图中4个半圆形磁场外无其他磁场(其中M1, M2点也无磁场),矩形M1N1M2N2区域外的磁场均可向其余区域扩展.
说明:只要在矩形区域M1N1N2 M2内除图中4个半圆形磁场外无其他磁场(其中M1, M2点也无磁场),矩形M1N1M2N2区域外的磁场均可向其余区域扩展. 
练习册系列答案
相关题目
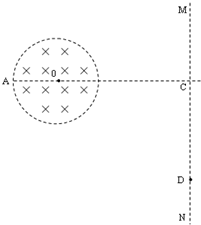 如图所示,真空中有一半径为R的圆形匀强磁场区域,圆心为O,磁场方向垂直于纸面向内,磁感应强度为B,距O点2R处有一屏MN,MN垂直于纸面放置,AO为垂直于屏的半径,其延长线与屏交于C.一个带负电的粒子以初速度V0沿AC方向进入圆形磁场区域,最后打在屏上D点,DC相距
如图所示,真空中有一半径为R的圆形匀强磁场区域,圆心为O,磁场方向垂直于纸面向内,磁感应强度为B,距O点2R处有一屏MN,MN垂直于纸面放置,AO为垂直于屏的半径,其延长线与屏交于C.一个带负电的粒子以初速度V0沿AC方向进入圆形磁场区域,最后打在屏上D点,DC相距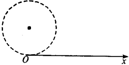 (2011?天门模拟)真空中有一半径为r的圆柱形匀强磁场区域,磁场方向垂直于纸面向里,Ox为过边界上O点的切线,如图所示.从O点在纸面内向各个方向发射速率均为V0的电子,设电子间相互作用忽略,且电子在磁场中的偏转半径也为r.已知电子的电荷量为e,质量为m.
(2011?天门模拟)真空中有一半径为r的圆柱形匀强磁场区域,磁场方向垂直于纸面向里,Ox为过边界上O点的切线,如图所示.从O点在纸面内向各个方向发射速率均为V0的电子,设电子间相互作用忽略,且电子在磁场中的偏转半径也为r.已知电子的电荷量为e,质量为m.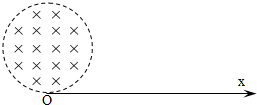 真空中有一半径为r的圆柱形匀强磁场区域,磁场方向垂直于纸面向里,ox为磁场边界上的切线,如图所示.从o点在纸面内向各个方向发射速率均为v0的带负电的粒子,设带电粒子间相互作用可忽略,且此种带负电的粒子在磁场中的偏转半径也是r.
真空中有一半径为r的圆柱形匀强磁场区域,磁场方向垂直于纸面向里,ox为磁场边界上的切线,如图所示.从o点在纸面内向各个方向发射速率均为v0的带负电的粒子,设带电粒子间相互作用可忽略,且此种带负电的粒子在磁场中的偏转半径也是r.
 于纸面向里,Ox为过边界O点的切线,如图所示,从O点在纸面内向各个方向发射速率均为
于纸面向里,Ox为过边界O点的切线,如图所示,从O点在纸面内向各个方向发射速率均为 的电子,设电子间相互作用忽略,且电子在磁场中的偏转半径也为r,已知电子的电荷量为e,质量为m。
的电子,设电子间相互作用忽略,且电子在磁场中的偏转半径也为r,已知电子的电荷量为e,质量为m。