题目内容
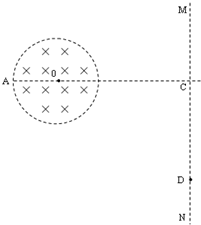 如图所示,真空中有一半径为R的圆形匀强磁场区域,圆心为O,磁场方向垂直于纸面向内,磁感应强度为B,距O点2R处有一屏MN,MN垂直于纸面放置,AO为垂直于屏的半径,其延长线与屏交于C.一个带负电的粒子以初速度V0沿AC方向进入圆形磁场区域,最后打在屏上D点,DC相距2
如图所示,真空中有一半径为R的圆形匀强磁场区域,圆心为O,磁场方向垂直于纸面向内,磁感应强度为B,距O点2R处有一屏MN,MN垂直于纸面放置,AO为垂直于屏的半径,其延长线与屏交于C.一个带负电的粒子以初速度V0沿AC方向进入圆形磁场区域,最后打在屏上D点,DC相距2| 3 |
(1)求粒子在磁场中运动的轨道半径r和粒子的荷质比.
(2)若该粒子仍以初速度V0从A点进入圆形磁场区域,但方向与AC成60°角且向右上方,粒子最后打在屏上E点,求粒子从A到E所经历的时间.
分析:(1)画出粒子运动的轨迹,根据几何关系及半径公式求解;
(2)粒子在磁场中做匀速圆周运动,根据转过的圆心角及周期公式即可求解在磁场中运动的时间,在磁场外做匀速直线运动,根据t=
即可求解时间,两个时间之和即为总时间.
(2)粒子在磁场中做匀速圆周运动,根据转过的圆心角及周期公式即可求解在磁场中运动的时间,在磁场外做匀速直线运动,根据t=
| s |
| v |
解答: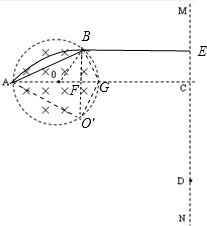
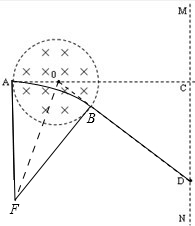 解:(1)粒子运动轨迹如图所示,在磁场中做匀速圆周运动,在磁场外做匀速直线运动,
解:(1)粒子运动轨迹如图所示,在磁场中做匀速圆周运动,在磁场外做匀速直线运动,
根据几何关系得:tan∠COD=
=
=
所以∠COD=60°
所以∠AFB=60°
则AF=
AO=
R
即粒子在磁场中运动的轨道半径r=
R
又因为r=
解得:
=
(2)粒子运动轨迹如图所示,在磁场中做匀速圆周运动,在磁场外做匀速直线运动,
根据几何关系可知:
粒子在磁场中运动的圆心角为60°,△AO′B是等边三角形,AB=AO′=BO′=
R,
B0′⊥AG,所以点F是OG的中点,即FG=
R,BE∥FC
在磁场中运动的时间为t1=
×
=
在磁场外运动的时间t2=
=
=
所以粒子从A到E所经历的时间为t=
+
答:(1)粒子在磁场中运动的轨道半径为
R,粒子的荷质比为
.
(2)粒子从A到E所经历的时间为t=
+

 解:(1)粒子运动轨迹如图所示,在磁场中做匀速圆周运动,在磁场外做匀速直线运动,
解:(1)粒子运动轨迹如图所示,在磁场中做匀速圆周运动,在磁场外做匀速直线运动,根据几何关系得:tan∠COD=
| CD |
| OC |
2
| ||
| 2R |
| 3 |
所以∠COD=60°
所以∠AFB=60°
则AF=
| 3 |
| 3 |
即粒子在磁场中运动的轨道半径r=
| 3 |
又因为r=
| mv |
| Bq |
解得:
| q |
| m |
| ||
| v0 |
(2)粒子运动轨迹如图所示,在磁场中做匀速圆周运动,在磁场外做匀速直线运动,
根据几何关系可知:
粒子在磁场中运动的圆心角为60°,△AO′B是等边三角形,AB=AO′=BO′=
| 3 |
B0′⊥AG,所以点F是OG的中点,即FG=
| 1 |
| 2 |
在磁场中运动的时间为t1=
| 1 |
| 6 |
| 2πr |
| v0 |
| ||
| 3v0 |
在磁场外运动的时间t2=
| FC |
| v0 |
R+
| ||
| v0 |
| 3R |
| 2v0 |
所以粒子从A到E所经历的时间为t=
| ||
| 3v0 |
| 3R |
| 2v0 |
答:(1)粒子在磁场中运动的轨道半径为
| 3 |
| ||
| v0 |
(2)粒子从A到E所经历的时间为t=
| ||
| 3v0 |
| 3R |
| 2v0 |
点评:本题是粒子在磁场中匀速圆周运动和场外做匀速直线运动的综合.磁场中圆周运动常用方法是画轨迹,由几何知识求半径.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,真空中有一垂直于纸面向里的匀强磁场,其边界为同心圆,内、外半径分别为r和R.圆心处有一粒子源不断地沿半径方向射出质量为m、电荷量为q的带电粒子,其速度大小为v,不计粒子重力.若
如图所示,真空中有一垂直于纸面向里的匀强磁场,其边界为同心圆,内、外半径分别为r和R.圆心处有一粒子源不断地沿半径方向射出质量为m、电荷量为q的带电粒子,其速度大小为v,不计粒子重力.若 如图所示,真空中有一匀强电场和水平面成一定角度斜向上,一个电荷量为Q=-5×10-6 C的点电荷固定于电场中的O处,在a处有一个质量为m=9×10-3 kg、电荷量为q=2×10-8C的点电荷恰能处于静止,a与O在同一水平面上,且相距为r=0.1m.现用绝缘工具将q搬到与a在同一竖直平面上的b点,Oa=Ob且相互垂直,在此过程中外力至少做功为( )
如图所示,真空中有一匀强电场和水平面成一定角度斜向上,一个电荷量为Q=-5×10-6 C的点电荷固定于电场中的O处,在a处有一个质量为m=9×10-3 kg、电荷量为q=2×10-8C的点电荷恰能处于静止,a与O在同一水平面上,且相距为r=0.1m.现用绝缘工具将q搬到与a在同一竖直平面上的b点,Oa=Ob且相互垂直,在此过程中外力至少做功为( ) 如图所示,真空中有一直角坐标系xOy,M、N分别是y轴和x轴上的两点.该空间内有一匀强电场,方向沿y轴负方向.一质量为m、电荷量为+q的粒子从M点以速度v0沿x轴正方向射出,恰能通过N点.已知OM=d,ON=2d,不计粒子重力.
如图所示,真空中有一直角坐标系xOy,M、N分别是y轴和x轴上的两点.该空间内有一匀强电场,方向沿y轴负方向.一质量为m、电荷量为+q的粒子从M点以速度v0沿x轴正方向射出,恰能通过N点.已知OM=d,ON=2d,不计粒子重力. (2010?安丘市模拟)如图所示,真空中有一束平行单色光射入厚度为h的玻璃砖,光与玻璃砖上表面的夹角为θ,入射光束左边缘与玻璃砖左端距离为b1,经折射后出射光束左边缘与玻璃砖的左端距离为b2,真空中的光速为c.则
(2010?安丘市模拟)如图所示,真空中有一束平行单色光射入厚度为h的玻璃砖,光与玻璃砖上表面的夹角为θ,入射光束左边缘与玻璃砖左端距离为b1,经折射后出射光束左边缘与玻璃砖的左端距离为b2,真空中的光速为c.则 如图所示,真空中有一电子束,以初速度v0沿着垂直场强方向从O点进入电场.以O点为坐标原点,垂直场强方向为x轴,沿场强方向为y轴建立坐标系.沿x轴取A、B、C三点,且OA=AB=BC,再自A、B、C点作y轴的平行线与电子径迹分别交于M、N、P点,则AM:BN:CP=
如图所示,真空中有一电子束,以初速度v0沿着垂直场强方向从O点进入电场.以O点为坐标原点,垂直场强方向为x轴,沿场强方向为y轴建立坐标系.沿x轴取A、B、C三点,且OA=AB=BC,再自A、B、C点作y轴的平行线与电子径迹分别交于M、N、P点,则AM:BN:CP=