题目内容
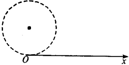 (2011?天门模拟)真空中有一半径为r的圆柱形匀强磁场区域,磁场方向垂直于纸面向里,Ox为过边界上O点的切线,如图所示.从O点在纸面内向各个方向发射速率均为V0的电子,设电子间相互作用忽略,且电子在磁场中的偏转半径也为r.已知电子的电荷量为e,质量为m.
(2011?天门模拟)真空中有一半径为r的圆柱形匀强磁场区域,磁场方向垂直于纸面向里,Ox为过边界上O点的切线,如图所示.从O点在纸面内向各个方向发射速率均为V0的电子,设电子间相互作用忽略,且电子在磁场中的偏转半径也为r.已知电子的电荷量为e,质量为m.(1)速度方向分别与Ox方向夹角成60°和90°的电子,在磁场中的运动时间分别为多少?
(2)所有从磁场边界射出的电子,速度方向有何特征?
(3)设在某一平面内有M、N两点,由M点向平面内各个方向发射速率均为V0的电子.请设计一种匀强磁场分布,使得由M点发出的所有电子都能够会聚到N点.
分析:(1)先画出粒子运动的轨迹,找出粒子运动的圆心角,根据圆心角与周期的关系求解时间;
(2)由轨迹图可知O2A与电子射出的速度方向垂直,电子射出方向一定与Ox轴方向平行,即所有的电子射出圆形磁场时,速度方向均与Ox轴相同;
(3)上题中从圆形磁场射出的这些速度相同的电子进入一相同的匀强磁场后,一定会聚焦于同一点磁场的分布如图所示,然后分对于从M点向MN连线上方运动的电子和对于从M点向MN连线下方运动的电子,根据半径与MN间的距离的关系即可求解.
(2)由轨迹图可知O2A与电子射出的速度方向垂直,电子射出方向一定与Ox轴方向平行,即所有的电子射出圆形磁场时,速度方向均与Ox轴相同;
(3)上题中从圆形磁场射出的这些速度相同的电子进入一相同的匀强磁场后,一定会聚焦于同一点磁场的分布如图所示,然后分对于从M点向MN连线上方运动的电子和对于从M点向MN连线下方运动的电子,根据半径与MN间的距离的关系即可求解.
解答: 解:(1)如图,入射时电子速度与x轴夹角为θ,无论入射击的速度方向与x轴的夹角为何值,由入射点O射出点A磁场圆心O1和轨道圆心O2一定组成边长为r的菱形.因O1O⊥OX,OO2垂直于入射速度,故∠OO2A=θ.即电子在磁场中所偏转的角度一定等于入射时电子速度与Ox轴的夹角.
解:(1)如图,入射时电子速度与x轴夹角为θ,无论入射击的速度方向与x轴的夹角为何值,由入射点O射出点A磁场圆心O1和轨道圆心O2一定组成边长为r的菱形.因O1O⊥OX,OO2垂直于入射速度,故∠OO2A=θ.即电子在磁场中所偏转的角度一定等于入射时电子速度与Ox轴的夹角.
当θ=60°时,t1=
=
.
当θ=90°时,t2=
=
.
(2)因∠OO2A=θ,故O2A⊥Ox.而O2A与电子射出的速度方向垂直,可知电子射出方向一定与Ox轴方向平行,即所有的电子射出圆形磁场时,速度方向均与Ox轴相同.
(3)上述的粒子路径是可逆的,(2)中从圆形磁场射出的这些速度相同的电子进入一相同的匀强磁场后,
一定会聚焦于同一点磁场的分布如图所示,对于从M点向MN连线上方运动的电子,两磁场分别与MN相切,M、N为切点,且平行于两磁场边界圆心的连线O1O2.设为l,所加的磁场的边界所对应圆的半径为r,故应有2r≤l,即
≤l,所以所加磁场磁感应强度应满足B≥
.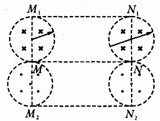
同理,对于从M点向MN连线下方运动的电子,只要使半径相同的两圆形磁场与止方的两圆形磁场位置关于MN对称且磁场方向
与之相反即可.
答:(1)速度方向分别与Ox方向夹角成60°和90°的电子,在磁场中的运动时间分别为
和
;
(2)所有从磁场边界射出的电子,速度方向均与Ox轴相同;
(3)如图所示.
 解:(1)如图,入射时电子速度与x轴夹角为θ,无论入射击的速度方向与x轴的夹角为何值,由入射点O射出点A磁场圆心O1和轨道圆心O2一定组成边长为r的菱形.因O1O⊥OX,OO2垂直于入射速度,故∠OO2A=θ.即电子在磁场中所偏转的角度一定等于入射时电子速度与Ox轴的夹角.
解:(1)如图,入射时电子速度与x轴夹角为θ,无论入射击的速度方向与x轴的夹角为何值,由入射点O射出点A磁场圆心O1和轨道圆心O2一定组成边长为r的菱形.因O1O⊥OX,OO2垂直于入射速度,故∠OO2A=θ.即电子在磁场中所偏转的角度一定等于入射时电子速度与Ox轴的夹角.当θ=60°时,t1=
| T |
| 6 |
| πr |
| 3v |
当θ=90°时,t2=
| T |
| 4 |
| πr |
| 2v |
(2)因∠OO2A=θ,故O2A⊥Ox.而O2A与电子射出的速度方向垂直,可知电子射出方向一定与Ox轴方向平行,即所有的电子射出圆形磁场时,速度方向均与Ox轴相同.
(3)上述的粒子路径是可逆的,(2)中从圆形磁场射出的这些速度相同的电子进入一相同的匀强磁场后,
一定会聚焦于同一点磁场的分布如图所示,对于从M点向MN连线上方运动的电子,两磁场分别与MN相切,M、N为切点,且平行于两磁场边界圆心的连线O1O2.设为l,所加的磁场的边界所对应圆的半径为r,故应有2r≤l,即
| 2mv |
| eB |
| 2mv |
| el |

同理,对于从M点向MN连线下方运动的电子,只要使半径相同的两圆形磁场与止方的两圆形磁场位置关于MN对称且磁场方向
与之相反即可.
答:(1)速度方向分别与Ox方向夹角成60°和90°的电子,在磁场中的运动时间分别为
| πr |
| 3v |
| πr |
| 2v |
(2)所有从磁场边界射出的电子,速度方向均与Ox轴相同;
(3)如图所示.
点评:本题主要考查了带电粒子在磁场中做匀速圆周运动的问题,要求同学们能画出粒子运动的轨迹,知道如何求小球在磁场中运动的时间,能熟练运用几何关系解题,难度较大,属于难题.

练习册系列答案
相关题目

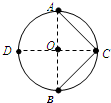 (2011?天门模拟)如图所示,AB、CD为一圆的两条直径,且相互垂直,O点为圆心.空间存在一未知静电场,场强方向与圆周所在平面平行.现有一电子,在电场力作用下(重力不计),先从A点运动到C点,动能减少了W;又从C点运动到B点,动能增加了W,那么关于此空间存在的静电场可能是( )
(2011?天门模拟)如图所示,AB、CD为一圆的两条直径,且相互垂直,O点为圆心.空间存在一未知静电场,场强方向与圆周所在平面平行.现有一电子,在电场力作用下(重力不计),先从A点运动到C点,动能减少了W;又从C点运动到B点,动能增加了W,那么关于此空间存在的静电场可能是( )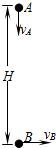 (2011?天门模拟)如图所示,小洁将小球甲从空中A点以υA=3m/s的速度竖直向下抛出,同时小明将另一小球乙从A点正下方H=10m的B点以υB=4m/s的速度水平抛出,不计空气阻力,B点离地面足够高,求两球在空中的最短距离.
(2011?天门模拟)如图所示,小洁将小球甲从空中A点以υA=3m/s的速度竖直向下抛出,同时小明将另一小球乙从A点正下方H=10m的B点以υB=4m/s的速度水平抛出,不计空气阻力,B点离地面足够高,求两球在空中的最短距离.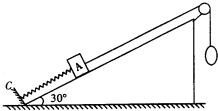 (2011?天门模拟)如图所示,在倾角为30°的光滑斜面上,一劲度系数为k的轻质弹簧一端固定在固定挡板C上,另一端连接一质量为m的物体A,一轻细绳通过定滑轮,一端系在物体A上,另一端有一细绳套,细绳与斜面平行,物体A处于静止状态.现在细绳套上轻轻挂上一个质量也为m的物体B,A将在斜面上做简谐运动.试求:
(2011?天门模拟)如图所示,在倾角为30°的光滑斜面上,一劲度系数为k的轻质弹簧一端固定在固定挡板C上,另一端连接一质量为m的物体A,一轻细绳通过定滑轮,一端系在物体A上,另一端有一细绳套,细绳与斜面平行,物体A处于静止状态.现在细绳套上轻轻挂上一个质量也为m的物体B,A将在斜面上做简谐运动.试求: