题目内容
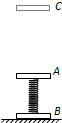 如图所示,A、B、C是三个完全相同的物块,质量均为m,其中物块A、B用轻弹簧相连,将它们竖直放在水平地面上处于静止状态,此时弹簧的压缩量为x0.已知重力加速度为g,物块的厚度及空气阻力均可忽略不计,且在下面所述的各过程中弹簧形变始终在弹性限度内.
如图所示,A、B、C是三个完全相同的物块,质量均为m,其中物块A、B用轻弹簧相连,将它们竖直放在水平地面上处于静止状态,此时弹簧的压缩量为x0.已知重力加速度为g,物块的厚度及空气阻力均可忽略不计,且在下面所述的各过程中弹簧形变始终在弹性限度内.(1)若用力将物块A竖直向上缓慢提起,使物块B恰好能离开水平地面,求此过程中物块A被提起的高度.
(2)如果使物块C从距物块A高3x0处自由落下,C与A相碰后,立即与A粘在一起不再分开,它们运动到最低点后又向上弹起,物块A刚好能回到使弹簧恢复为原长的位置.求C与A相碰前弹簧的弹性势能大小.
(3)如果将物块C从距物块A上方某处由静止释放,C与A相碰后立即一起向下运动但并不粘连.此后物块A、C在弹起过程中分离,其中物块C运动到最高点时被某装置接收,而物块A刚好能在物块B不离开地面的情况下做简谐运动.求物块C的释放位置与接收位置间的距离.
分析:(1)由胡克定律分别求出AB竖直放置静止时,弹簧被压缩的长度和物块B恰好能离开水平地面时,弹簧伸长的长度,由几何关系求解物块A被提起的高度.
(2)物块C从距物块A高3x0处自由落下机械能守恒,C与A碰撞过程遵守动量守恒,C与A相碰后一起向下运动到最低点,然后反弹至弹簧原长的过程,CA和弹簧组成的系统机械能守恒,分别列方程求出C与A相碰前弹簧的弹性势能大小.
(3)根据问题(2)同样分析,结合物块A刚好能在物块B不离开地面的情况下做简谐运动的条件,按过程列方程,求出物块C的释放位置与接收位置间的距离.
(2)物块C从距物块A高3x0处自由落下机械能守恒,C与A碰撞过程遵守动量守恒,C与A相碰后一起向下运动到最低点,然后反弹至弹簧原长的过程,CA和弹簧组成的系统机械能守恒,分别列方程求出C与A相碰前弹簧的弹性势能大小.
(3)根据问题(2)同样分析,结合物块A刚好能在物块B不离开地面的情况下做简谐运动的条件,按过程列方程,求出物块C的释放位置与接收位置间的距离.
解答:解:(1)设弹簧劲度系数为k,物块A、B用轻弹簧相连,竖直放置时,弹簧的压缩量为x0=
.
将物块A竖直向上缓慢提起,使物块B恰好能离开水平地面时,
弹簧伸长x1=
则物块A被提起的高度L=x0+x1=2x0
(2)设C自由落下到与A相碰前的速度为v1,由机械能守恒定律,得
mg?3x0=
m
设C与A碰撞后一起向下运动的初速度为v2,根据动量守恒定律,得
mv1=2mv2
设C与A相碰前弹簧的弹性势能为EP,物块A、C运动到最低点后又向上反弹,刚好能使弹簧恢复到原长的过程中,对A、C和弹簧组成的系统机械能守恒得
有
2m
+EP=2mgx0
联立解
EP=
mgx0
(3)设物块C距物块A的高度差为h0,与物块A碰撞前速度为v3,由机械能守恒定律得
mgh0=
m
设C与A相碰后一起向下运动的初速度为v4,根据动量守恒定律有
mv3 =2mv4
物块A、C一起向下压缩弹簧后向弹起,到达弹簧原长时,C与A分离.设分离时速度为v5,对此过程由机械能守恒定律,得
2
+EP=2mgx0+
2m
之后,物块C向上做匀减速运动,设上升的高度为h,则根据机械能守恒定律有
m
=mgh 解得h=
因物块A刚好能在物块B不离开地面的情况下做简谐运动,结合第(1)问可知,物块A运动到最高点时,弹簧形变量为x0,故物块A运动到最高点时弹簧的弹性势能与物块A处于静止状态弹簧的弹性势能相等.
对物块A从弹簧恢复原长位置运动到最高点过程中,由机械能守恒定律有
m
=mgx0+EP
联立以上各式,解得h0=9x0,h=1.5x0
由几何关系可知,物块C的释放位置与接收位置间的距离
△h=h0-x0-h=6.5x0
| mg |
| k |
将物块A竖直向上缓慢提起,使物块B恰好能离开水平地面时,
弹簧伸长x1=
| mg |
| k |
(2)设C自由落下到与A相碰前的速度为v1,由机械能守恒定律,得
mg?3x0=
| 1 |
| 2 |
| v | 2 1 |
设C与A碰撞后一起向下运动的初速度为v2,根据动量守恒定律,得
mv1=2mv2
设C与A相碰前弹簧的弹性势能为EP,物块A、C运动到最低点后又向上反弹,刚好能使弹簧恢复到原长的过程中,对A、C和弹簧组成的系统机械能守恒得
有
| 1 |
| 2 |
| v | 2 2 |
联立解
EP=
| 1 |
| 2 |
(3)设物块C距物块A的高度差为h0,与物块A碰撞前速度为v3,由机械能守恒定律得
mgh0=
| 1 |
| 2 |
| v | 2 3 |
设C与A相碰后一起向下运动的初速度为v4,根据动量守恒定律有
mv3 =2mv4
物块A、C一起向下压缩弹簧后向弹起,到达弹簧原长时,C与A分离.设分离时速度为v5,对此过程由机械能守恒定律,得
| 1 |
| 2 |
| mv | 2 4 |
| 1 |
| 2 |
| v | 2 5 |
之后,物块C向上做匀减速运动,设上升的高度为h,则根据机械能守恒定律有
| 1 |
| 2 |
| v | 2 5 |
| ||
| 2g |
因物块A刚好能在物块B不离开地面的情况下做简谐运动,结合第(1)问可知,物块A运动到最高点时,弹簧形变量为x0,故物块A运动到最高点时弹簧的弹性势能与物块A处于静止状态弹簧的弹性势能相等.
对物块A从弹簧恢复原长位置运动到最高点过程中,由机械能守恒定律有
| 1 |
| 2 |
| v | 2 5 |
联立以上各式,解得h0=9x0,h=1.5x0
由几何关系可知,物块C的释放位置与接收位置间的距离
△h=h0-x0-h=6.5x0
点评:本题是比较复杂的力学综合题,首先要确定研究对象,其次分析物理过程,并寻找各个物理过程遵循的物理规律,同时要挖掘隐含的条件.

练习册系列答案
相关题目

 如图所示,a、b、c为电场中同一电场线上的三点,且b为ac的中点,a、c电势分别为φa=8V,φc=6V.下列叙述正确的是( )
如图所示,a、b、c为电场中同一电场线上的三点,且b为ac的中点,a、c电势分别为φa=8V,φc=6V.下列叙述正确的是( ) 如图所示,A、B、C、D是某匀强电场中的4个等势面,一个质子和一个α粒子(电荷量是质子的2倍,质量是质子的4倍)同时在A等势面从静止出发,向右运动,当到达D等势面时,下列说法正确的是( )
如图所示,A、B、C、D是某匀强电场中的4个等势面,一个质子和一个α粒子(电荷量是质子的2倍,质量是质子的4倍)同时在A等势面从静止出发,向右运动,当到达D等势面时,下列说法正确的是( ) 如图所示,a、b和c都是厚度均匀的平玻璃板,a和b、b和c之间的夹角都为α,一细光束由红光和蓝光组成,以入射角θ从O点射入a板,且射出c板后的两束单色光通过空气射在地面上P、Q两点,由此可知( )
如图所示,a、b和c都是厚度均匀的平玻璃板,a和b、b和c之间的夹角都为α,一细光束由红光和蓝光组成,以入射角θ从O点射入a板,且射出c板后的两束单色光通过空气射在地面上P、Q两点,由此可知( )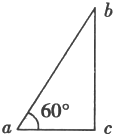 如图所示,a、b、c是匀强电场中的直角三角形的三个顶点.已知a、b、c三点的电势分别为φa=8V、φb=-4V、φc=2V,
如图所示,a、b、c是匀强电场中的直角三角形的三个顶点.已知a、b、c三点的电势分别为φa=8V、φb=-4V、φc=2V,