题目内容
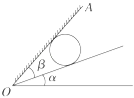
【题目】劳伦斯和利文斯设计出回旋加速器,工作原理示意图如图所示。置于真空中的D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过的时间可忽略。磁感应强度为B的匀强磁场与盒面垂直,高频交流电频率为f,加速电压为U。若A处粒子源产生的质子质量为m、电荷量为+q,在加速器中由静止被加速,且加速过程中不考虑相对论效应和重力的影响。则下列说法正确的是( )
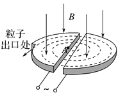
A.质子被加速后的最大速度不可能超过2πfR
B.质子离开回旋加速器时的最大动能与加速电压U成正比
C.质子第2次和第1次经过两D形盒间狭缝后轨道半径之比为![]() ∶1
∶1
D.不改变磁感应强度B和交流电频率f,只改变加速电压U,该回旋加速器的最大动能不变
【答案】ACD
【解析】
A.质子出回旋加速器的速度最大,此时的运动半径为![]() ,则有质子被加速后的最大速度:
,则有质子被加速后的最大速度:
![]()
所以最大速度不超过![]() ,故A正确;
,故A正确;
B.粒子在磁场中做匀速圆周运动,由牛顿第二定律得:
![]()
可得:
![]()
则最大动能为:
![]()
与加速的电压无关,故B错误;
C.质子在加速电场中做匀加速运动,根据动能定理有:
![]()
解得:
![]()
质子第二次和第一次经过D形盒狭缝的速度比为:
![]()
根据![]() 可得质子第2次和第1次经过两D形盒间狭缝后轨道半径之比为:
可得质子第2次和第1次经过两D形盒间狭缝后轨道半径之比为:
![]()
故C正确;
D.根据最大动能![]() ,可知不改变磁感应强度
,可知不改变磁感应强度![]() 和交流电频率
和交流电频率![]() ,只改变加速电压
,只改变加速电压![]() ,该回旋加速器的最大动能不变,故D正确;
,该回旋加速器的最大动能不变,故D正确;
故选ACD。

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案【题目】如图所示,某实验小组同学利用DIS实验装置研究支架上力的分解,A、B为两个相同的双向力传感器,该型号传感器在受到拉力时读数为正,受到压力时读数为负。A连接质量不计的细绳,可沿固定的板做圆弧形移动;B固定不动,通过光滑铰链连接长0.3 m的杆;将细绳连接在杆右端D点构成支架。保持杆在水平方向,g取10 m/s2,按如下步骤操作:
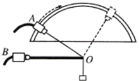
①测量绳子与水平杆的夹角∠AOB=θ;
②对两个传感器进行调零;
③用另一根绳在D点悬挂一个钩码,记录两个传感器的读数;
④取下钩码,移动传感器A改变θ角。
重复上述实验步骤,得到表格。
F1/N | 1.001 | 0.580 | … | 1.002 | … |
F2/N | -0.868 | -0.291 | … | 0.865 | … |
θ | 30 | 60 | … | 150 | … |
(1)根据表格,A传感器对应的是表中力_____(填“F1”或“F2”);钩码质量为______kg(保留一位有效数字)。
(2)本实验中多次对传感器进行调零,对此操作说明正确的是________。
A.因为事先忘记调零
B.何时调零对实验结果没有影响
C.为了消除横杆自身重力对结果的影响
D.可以完全消除实验的误差